Neal Stephenson - Peanatema

Trójkątna arka:Inne określenie kelksu lub jednej z jego ark.

Tum:W wielu koncentach duży, centralnie ulokowany budynek, mieszczący zegar i wykorzystywany podczas rytów i innych zgromadzeń mieszkańców koncentu.

Twierdzenie Adrakhonesa:Stare twierdzenie w geometrii płaskiej, przypisywane Adrakhonesowi, założycielowi Oritheny, i postulujące, że w trójkącie prostokątnym kwadrat długości przeciwprostokątnej jest równy sumie kwadratów długości przyprostokątnych. Na Ziemi jego odpowiednikiem jest twierdzenie Pitagorasa.

Tysięcznik:Potocznie milenarysta (zob.).

Unarysta:Deklarant, który przysiągł nie opuszczać matemu i unikać kontaktów ze światem zewnętrznym aż do następnego apertu rocznego. Potocznie: „jednorazowiec”.

Uraloabus:Najsłynniejszy sfenik Złotego Wieku Ethras, który — jeśli wierzyć relacji Protasa — popełnił samobójstwo po splantowaniu przez Thelenesa.

Urządzenie syntaktyczne:Odpowiednik ziemskiego komputera.

Uthentine:Suur z Saunty Baritoe z czternastego wieku p.r., która wspólnie z Erasmasem stworzyła gałąź metateoryki nazwaną protyzmem złożonym.

Voco:Rzadko odprawiany ryt, w którym państwo sekularne powołuje (wzywa z matemu) deklaranta, którego talenty są niezbędne w Saeculum. Tylko w wyjątkowych wypadkach zdarza się, żeby powołany deklarant wrócił do świata matemowego.

Wielka Trójka:Trzy koncenty — Saunt Muncoster, Saunt Tredegarh i Saunta Baritoe; stare, zamożne, wybitne i połączone bliskimi związkami.

Zwiastun:Jeden z trzech kataklizmów, które w ostatnich dekadach Epoki Praksis przetoczyły się przez większą część Arbre, a z biegiem czasu zostały zinterpretowane jako ostrzeżenie przed Straszliwymi Wypadkami. Dokładny charakter zwiastunów trudno określić po tym, jak wszystkie zapiski na ich temat uległy zniszczeniu (wiele z nich przechowywano w urządzeniach syntaktycznych, które później przestały działać), ale według powszechnie akceptowanej teorii pierwszym zwiastunem był wybuch licznych rewolucji na całym świecie, drugim — wojna światowa, trzecim zaś — ludobójstwo.

— Przypuśćmy, że każda porcja ma mieć kształt kwadratu i szerokość łopatki do ciasta — powiedziałem. — Wykrój, proszę, cztery takie kawałki w narożniku blachy.

Dath naciął ciasto w taki sposób:

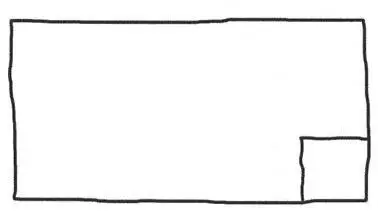
a następnie pokroił je na cztery części, tak jak prosiłem:

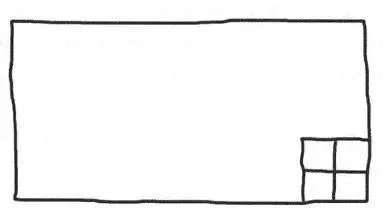
— Nie mogę uwierzyć, że naprawdę to robisz — mruknął Arsibalt.

— Skoro Thelenesowi się udało… — odmruknąłem. — Siedź cicho. — Odwróciłem się do Datha, który czekał na dalsze instrukcje. — Ile porcji mamy?

— Cztery — odparł, trochę zdeprymowany moim niedorzecznie łatwym pytaniem.

— A co by się stało, gdybyś wykroił taką samą figurę, tylko z dwa razy dłuższą krawędzią? Tak żeby zamiast dwóch jednostek, czyli dwóch szerokości łopatki, długość boku kwadratu liczyła…?

— Cztery?

— No właśnie. W tej chwili mamy cztery kawałki. Jeżeli wydłużysz bok kwadratu dwukrotnie, ile porcji dostaniesz?

— To proste: dwa razy cztery równa się osiem.

— Tu się zgadzam: dwa razy cztery równa się osiem. Krój.

Dath pokroił ciasto jak następuje:

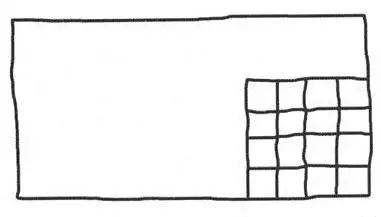
Już w połowie krojenia zorientował się, że popełnił błąd. Skrzywił się, ale przekonałem go, żeby doprowadził sprawę do końca.

— Szesnaście — powiedział. — Dostaliśmy szesnaście porcji, nie osiem.

— Podsumujmy. Kiedy wykrawamy kwadrat o boku dwóch jednostek, ile porcji dostajemy?

— Cztery.

— Przed chwilą powiedziałeś mi, że z kwadratu o boku czterech jednostek dostaniemy szesnaście, tak? A co musielibyśmy zrobić, żeby uzyskać tylko osiem porcji? Jaką kratkę musiałbyś narysować?

— Trzy na trzy? — zapytał ostrożnie Dath. Spojrzał na ciasto, policzył. — Nie, to by było dziewięć.

— Ale jesteśmy blisko. Poza tym nastąpiła pewna istotna zmiana: wiesz, że nie wiesz.

Dath uniósł brwi.

— To ważne?

— Dla nas, tutaj, nawet bardzo.

Nie pamiętałem, jaki był następny ruch Thelenesa, kiedy sześć tysięcy lat temu przedstawiał to ćwiczenie małemu niewolnikowi na Płaszczyźnie. Musiałem zapytać Orola.

Odwróciłem blachę, podsuwając Dathowi świeży narożnik.

— Wytnij kwadrat, który wystarczyłby na cztery kawałki — poleciłem. — Nie musisz go dzielić na porcje.

— A mogę zaznaczyć linie na lukrze?

— Jeśli ci to pomoże…

Z pomocą Cord Dath zrobił coś takiego:

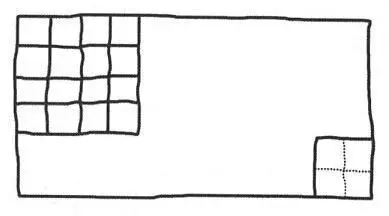
— Bardzo dobrze — pochwaliłem. — Dołóż teraz jeszcze trzy takie kwadraty.

Dath przedłużył niektóre cięcia, dodał nowe i uzyskał następujący rezultat:

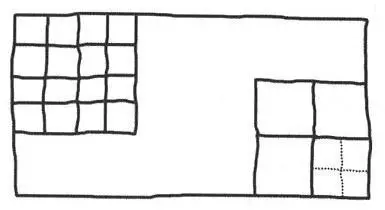
— Bądź tak miły i przypomnij mi, ile porcji możemy uzyskać z takiego kawałka?

— Szesnaście.

— Zgadza się. Skupmy się na chwilę na tym mniejszym kwadracie, w samym rogu.

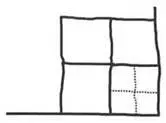
— Umiałbyś go podzielić jednym cięciem dokładnie na pół?

Dath przyłożył łopatkę do jednej z zaznaczonych na lukrze linii. Pokręciłem głową.

— Arsibalt, który tu koło mnie siedzi, bardzo lubi ciasto i nie chciałby, żeby ktoś dostał większy kawałek od niego — powiedziałem.

— Dzięki ci, o przemądry Thelenesie — wtrącił Arsibalt.

Udałem, że go nie słyszę.

— Umiesz tak pokroić ten kawałek jednym cięciem, żeby zadowolić Arsibalta? Porcje nie muszą być kwadratowe, inne kształty też są do przyjęcia. Na przykład trójkąty.

Po tej wskazówce Dath przekroił ciasto tak:

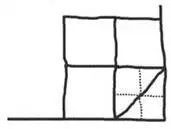
— Pokrój też trzy pozostałe — poprosiłem. Wyszło tak:

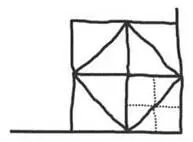
— Kiedy przekroiłeś kwadrat po przekątnej, przeciąłeś go dokładnie na pół, prawda?

— Tak.

— Czy to samo można powiedzieć o pozostałych trzech kwadratach i trzech cięciach na skos?

— Oczywiście.

— Dobrze. Pozwól, że obrócę teraz blachę.

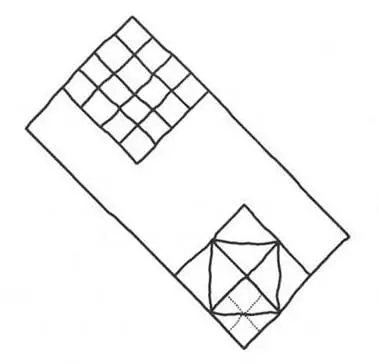
— Jaki kształt widzisz w środku tego dużego kwadratu, u dołu blachy?

— Też kwadrat.

— Ile porcji zawiera?