Виталий Морозков - Настольная игра «Футбол на бумаге»

7). Дано:ты договариваешься с противником о проведении матча.

Определить:на каком количестве партий в матче тебе нужно настаивать, чтобы твои шансы на успехбыли максимальными.

Решение:

Матч может состоять из нечётногоили чётногоколичества партий. Поскольку в отдельной футбольной партии ничьи быть не может,то в нечётном матче всегда определяется победитель. В матче же, состоящем из чётного количества партийигроки могут сыграть в ничью. Для победы в матче требуется выиграть абсолютное большинство партий:

-для нечётного матча – kпартий из n , где ( n +1)/2 k n;

-для чётного матча – fпартий из m , где m /2+1 f m

Введём несколько понятий:

– нечётный матч– матч, состоящий из нечётного количества партий.

- чётный матч– матч, состоящий из чётного количества партий.

Определение «формулы» матча зависит от нескольких обстоятельств:

1).Тебе нужна победа в матче или тебя устроит и ничья (т.е. игра будет вестись на победуили на непоражение); т.к. выиграть матч, состоящий из нечётного количества партий N, меньше шансов, чем не проиграть матч, состоящий из чётного количества партий ( N +1).

Для наглядности можно привести простой пример:

Перед тобой дилемма– выбирать матч, состоящий из однойили из двухпартий. Очевидно, что более надёжный вариант– это две партии,поскольку даже если ты проиграешь в первой партии– возможно тебе удастся отыграться во второйи свести матч вничью. Но, если тебе в силу тех или иных обстоятельств нужна только победа, конечно лучше играть одну партию. Таким образом, здесь всё зависит от твоей цели.

2).Знаешь ли ты свои шансы на победу в одной партии.

3).Если знаешь то каковы они ( меньшеили больше,чем у противника, или равны).

1. Допустим, что ты знаешь свои шансы на победу в отдельной партии:

- Н 1 ( n )– вероятность не проиграть в матче, состоящем из nпартий, для первого игрока

- Н 2 ( n )– вероятность не проиграть в матче, состоящем из nпартий, для второго игрока

- В 1 ( n )– вероятность выиграть в матче, состоящем из nпартий, для первого игрока

- В 2 ( n )– вероятность выиграть в матче, состоящем из nпартий, для второго игрока

- Д( n )– вероятность того, что игроки сыграют в ничью матч из nпартий ( n– всегда чётное)

1.1.Вероятность того, что матч выиграетодин из игроков или он закончится в ничью(если это чётный матч) равна 1. Пускай в нашем небольшом исследовании 1будет равна 729 (3 6 ) шансам.

Допустим, что: Н 1 (1)=В 1 (1)=1/3;тогда Н 2 (1)=В 2 (1)=2/3.Т.е. вероятность выиграть для первого игрока в одной партии равна 243 шансам,для второго – 486 шансам.Тогда:

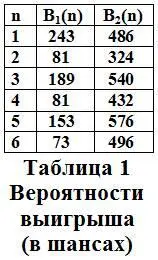
Выводы из таблиц 1 и 2:

1).Шансов выиграть в нечётном матче из nпартий больше, чем в чётном из ( n +1)партий;

2).Шансы на выигрыш у более слабого игрока с увеличением количества партий «тают на глазах»,а у более сильного игрока наоборот возрастают;

3).Шансов не проиграть в чётном матче из nпартий больше, чем в нечётном из ( n -1)партий;

4).Шансы на непроигрыш у более слабого игрока с увеличением количества партий также становятся меньше,а у более сильного игрока возрастают.