Виталий Морозков - Настольная игра «Футбол на бумаге»

ЧВ(В), ЧВ(Н)– чётный выход в пользу Верхнего (В) или Нижнего игрока (Н);

Х– конец партии.

Прежде чем перейти к изучению математических особенностей игры необходимо ввести определение размеров футбольного поля.

Размеры симметричного футбольного поля– это числовая совокупность вида ( n 1; n 2; n 3), где n 1, n 2, n 3– это:

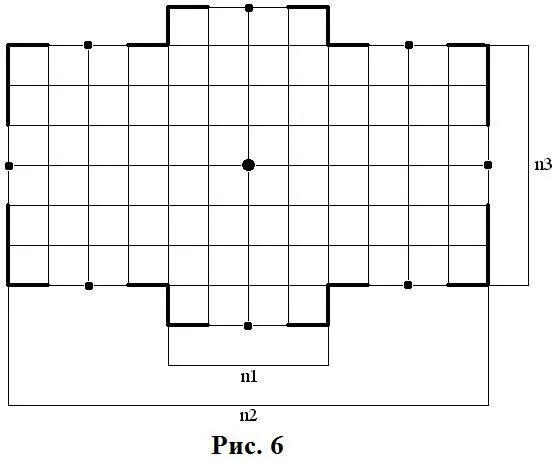
Таким образом, наше футбольное поле имеет размеры (2;6;8).

1). Дано:симметричное футбольное поле размера ( n 1; n 2; n 3).

Определить:количество незанятых пересечений – N.

Решение:из рисунка 6очевидно, что: N =2( n 1-1)+( n 2-1)( n 3-1)-1

для нашего футбольного поля: N =2(2-1)+(6-1)(8-1)-1=36

2). Дано:симметричное футбольное поле размера ( n 1; n 2; n 3).

Доказать:на данном поле всегда чётное количество незанятых пересечений.

Доказательство:т.к. поле симметрично, то очевидно, что n 1, n 2, n 3– всегда являются чётными числами. Введём обозначения: Н– нечётное число; Ч– чётное число. Тогда:

Из формулы определения количества пустых пересечений следует:

N =Ч(Ч-Н)+(Ч-Н)(Ч-Н)-Н=ЧН+НН-Н=Ч+Н-Н=Н-Н=Ч

Таким образом, N =Чвсегда.

3). Дано:диаграмма с изображением сыгранной партии или части партии.

Определить:сколько было сделано ходов.

Решение:т.к. игрок ходит до тех пор пока маршрут хода не попадёт в пустое пересечение – очевидно, что, подсчитав количество пересечений, превратившихся из пустых в занятые, мы определим и количество совершённых ходов.

На рисунке 7-1дана диаграмма сыгранной партии, а на рисунке 7-2показаны «превратившиеся»пересечения (они обозначены красным цветом).

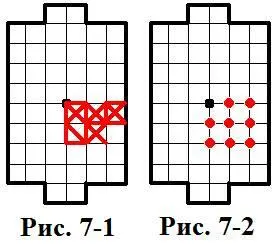
Обозначим количество «превратившихся»пересечений через P. Из рисунка 7-2очевидно, что: Р=33-1=8

Таким образом, в партии было сделано 8 ходов.

4). Дано:диаграмма с изображением сыгранной партии или части партии.

Доказать: 1.количество рёбер, исходящих из центра поля и последнего занятого пересечения всегда нечётно;

2.количество рёбер, исходящих из любого другого занятого пересечения всегда чётно.

Ребро– отрезок, соединяющий два занятых пересечения.

Доказательство:

1.первый ход делается из центра поля (например d 6- d 7). Таким образом, после первого хода из центра поля исходит одно ребро.При дальнейшей игре «встав»в центр поля игрок должен от него «оттолкнуться».

Обозначим количество рёбер, исходящих из центра поля, через С.Тогда очевидно, что: С=1+2+…+2=Н+Ч+…+Ч=Н+Ч=Н

Максимальное количество рёбер, исходящих из центра поля, равно 7(после трёх прохождений через центр, на четвёртом игрок попадает в тупик).

Очевидно, что количество рёбер, исходящих из последнего занятого пересечения равно 1, а следовательно нечётно.

2.Пересечения не являющиеся ни последними, ни центром поля сами были последними, но потом из них делали ход, т.е. количество рёбер, исходящих из данных пересечений, становилось равным 2. При дальнейшей игре «встав»в данное пересечение игрок должен от него «оттолкнуться».Обозначим количество рёбер, исходящих из такого пересечения (которое не является ни последним, ни центром поля), через S. Тогда очевидно, что:

S=2+2+…+2= Ч + Ч +…+ Ч = Ч