Виталий Морозков - Настольная игра «Футбол на бумаге»

3 – угловые пересечения ( a 2; g 2; a 10; g 10):

Очевидно, что данные пересечения являются нечётными,поскольку от них отходит всего одна грань,заняв которую ты попадаешь в тупик.

4 – полевые пересечения (( b 3-… b 9;…; f 3-… f 9) – кроме d 6):

Эти пересечения в начале партии являются пустымии по ходу игры «превращаются» в занятые.Это происходит следующим образом: одна из сторон занимает полевое пересечение и в нём «останавливается»,затем другая сторона ходит из этого пересечения. Т.о. от полевого пересечения будут отходить шесть незанятых граней (рис. 16):

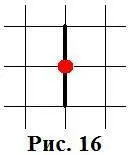
При дальнейшей игре, заняв полевое пересечение, нужно от него «оттолкнуться»,т.е. каждый раз будут заниматься две грани: 6:2=2×3

Т.е. после трёх прохожденийчерез полевое пересечение ты займёшь все грани и дальнейший проход в такое пересечение невозможен. То есть, в полевом пересечении нельзя попасть в тупик,оно является чётным.

5, 6 – околоворотные пересечения ( c 2; c 10; e 2; e 10; d 2; d 10):

Часть рёбер, исходящих от данных пересечений, соединена с воротными пересечениями,т.е. с пересечениями, заняв которые одной из сторон автоматически засчитывается поражение. Таким образом, условие тупиковости (нечётности)для околоворотных пересеченийне может быть выполнено и они являются чётными.

Если бы в ФУТБОЛЕ НА БУМАГЕ отсутствовало правило гола – то 6пересечения ( c 2; c 10; e 2; e 10)превратились бы в тупиковые(поскольку от них отходят пять незанятых граней), а 5пересечения ( d 2; d 10)остались бы также чётнымии были бы простыми полевыми пересечениями.

Теперь давай представим результаты в графическом виде ( нечётныеи воротные пересеченияизображены красным цветом, чётные – чёрным):

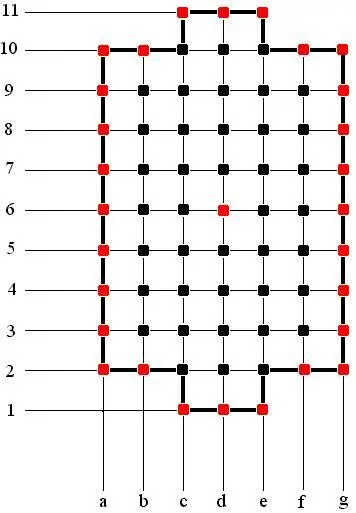
Таким образом, если партия ведётся строго по правилам и доигрывается до победного конца – последним занимается одно из красных пересечений.

6). Следствие нечётности пересечений:

а).Введём определение изолированной группы:

изолированная группа– это конструкция, при которой проход к обоим воротам полностью перекрыт.Пример изолированной группы показан на рисунке 17.

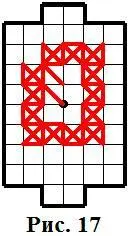
б). Внутри изолированной группы всегда есть хотя бы одно нечётное пересечение.Это вполне очевидно – ведь если проход к обоим воротам полностью перекрыт, то в итоге одна из сторон попадёт в тупик,т.е. займёт тупиковое (нечётное) пересечение.

В примере представленном на рисунке 17таким пересечением является центр.

Дано:симметричное футбольное поле произвольного размера

Доказать:на данном поле нельзя построить конструкцию следующего вида:

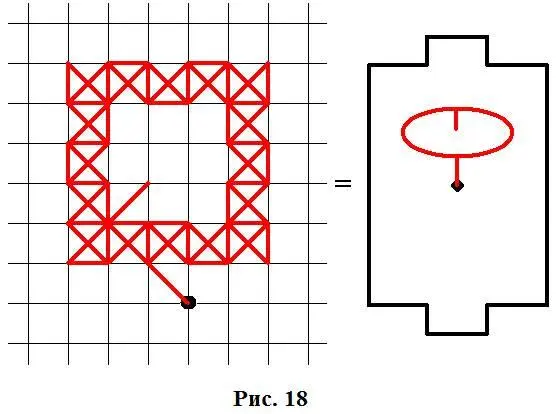
Доказательство:допустим, что такую конструкцию можно построить, тогда внутри неё должно быть хотя бы одно нечётное пересечение,но таких пересеченийвнутри данной конструкции нет,а есть только полевые пересечения,которые являются чётными,в чётном пересечении нельзя попасть в тупик.Мы пришли к противоречию– следовательно, такую конструкцию нельзя построить,если строго соблюдать правила ФУТБОЛА НА БУМАГЕ. Приведённая на рисунке 18конструкция построена с нарушением правил игры.

Данное утверждение справедливо для футбольных полей любых конфигураций, необходимо только, чтобы совпадала «внутренняя геометрия».