Мартин Гарднер - А ну-ка, догадайся!

1. Парадокс Греллинга назван в честь открывшего его немецкого математика Курта Греллинга. Разделим все прилагательные на два множества: самодескриптивные, обладающие тем свойством, которое они выражают, и несамодескриптивные. Такие прилагательные, как «многосложное», «русское» и «видимое», принадлежат к числу самодескриптивных, а такие прилагательные, как «односложное», «немецкое» и «невидимое», — к числу несамодескриптивных. К какому из двух множеств принадлежит прилагательное «несамодескриптивнсе»?

2. Парадокс Берри назван в честь библиотекаря Оксфордского университета Дж. Дж. Берри, который сообщил его Расселу. В парадоксе Берри речь идет о «наименьшем целом числе, которое не может быть задано менее чем тринадцатью словами». Выражение, взятое в кавычки, содержит 12 слов. Какому множеству принадлежит определяемое им выражение: множеству целых чисел, которые на русском языке задаются менее чем 13 словами, или множеству целых чисел, задаваемых на русском языке 13 и более словами? Любой из двух ответов приводит к противоречию.

3. Философ Макс Блэк сформулировал парадокс Берри примерно так. В этой книге упоминаются различные целые числа. Сосредоточим наше внимание на наименьшем целом числе, которое ни прямо, ни косвенно не упоминается в этой книге. Существует ли такое число?

Одни люди интересные, другие скучные.

Футболист.Я лучший нападающий США.

Музыкант.Я умею играть на гитаре ногами.

М-р Скучмен.Я ничего не умею.

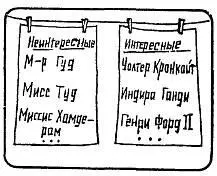
Мы составили два списка. В один внесли всех скучных людей, в другой — всех интересных людей.

Где-то в списке скучных людей числится самый скучный человек в мире.

Но именно этим он и интересен, поэтому мы должны вычеркнуть его из списка скучных людей и занести в список интересных людей.

М-р Скучмен.Благодарю вас. Но теперь в списке скучных людей где-то затерялся самый скучный человек среди оставшихся, который этим и интересен. Так постепенно каждый скучный человек станет интересным. Станет ли, как вы думаете?

Этот забавный парадокс представляет собой вариант «доказательства» того, что каждое положительное целое число чем-то интересно. Впервые оно было опубликовано Эрвином Ф. Бекенбахом в заметке «Интересные целые числа» в апрельском номере журнала American Mathematical Monthly за 1945 г.

Верно ли такое «доказательство» и не таит ли оно в себе логической ошибки? Не перейдет ли снова в разряд скучных человек, чье имя было первым включено в список интересных людей и вычеркнуто из списка скучных людей после того, как список интересных людей пополнится вторым среди самых скучных людей? Можно ли придать какой-то смысл утверждению о том, что каждый человек интересен, поскольку он является самым скучным из людей, образующих определенные множества, подобно тому как каждое целое число является наименьшим числом в определенных множествах чисел? Если все люди (или числа) интересны, то не утрачивает ли от этого смысл прилагательное «интересный»?

Парадоксы, связанные со значениями истинности, называются семантическими, парадоксы, связанные с множествами каких-то объектов, — теоретико-множественными. Оба типа парадоксов тесно связаны.

Соответствие между семантическими и теоретико-множественными парадоксами проистекает из того, что любое истинное или ложное утверждение можно представить в виде некоего утверждения о множествах и наоборот. Например, утверждение «Все яблоки красные» означает, что множество всех яблок содержится в множестве всех красных предметов. На языке высказываний, относительно которых можно утверждать, что они истинны или ложны, это переводится так: «Если верно, что х— яблоко, то верно, что хкрасного цвета».