Мартин Гарднер - А ну-ка, догадайся!

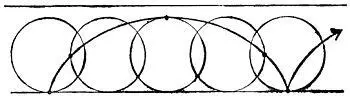
Циклоида обладает множеством красивых математических и механических свойств. Одна из глав моей «Шестой книги математических забав» из журнала Scientific American называется «Циклоида — Елена Прекрасная геометрии». В ней, в частности, рассказывается, как начертить циклоиду с помощью катящейся банки из-под кофе. Построим циклоиду и выведя ее уравнение, вы сможете лучше оценить изящество этой кривой и ее необычные свойства.

Лыжник.Какой великолепный день! Вот если бы только скорость подъемника была больше 5 км/ч!

Предположим, что лыжник захочет поднять среднюю скорость, развиваемую на подъеме и спуске, до 10 км/ч. С какой скоростью он должен съезжать с горы?

15 км/ч? 60 км/ч? 100 км/ч? Хотя в это трудно поверить, но единственный способ поднять среднюю скорость до 10 км/ч для лыжника состоит в том, чтобы съехать за нулевое время!

Сначала кажется, что решение парадокса как-то связано с расстоянием, проходимым лыжником при подъеме и спуске. Но в действительности оно несущественно. Лыжник преодолевает какое-то расстояние, поднимаясь на гору, и хотел бы спуститься со скоростью, при которой средняя скорость при подъеме и спуске была бы вдвое больше скорости при подъеме.

Чтобы развить такую среднюю скорость, лыжнику пришлось бы преодолеть вдвое большее расстояние (туда и обратно), чем он преодолел при подъеме, за то же время, которое он затратил на подъем. Следовательно, на спуск у нашего лыжника просто нет времени: он должен был бы преодолеть склон за нулевое время! Поскольку это невозможно, лыжник никаким способом не может поднять свою среднюю скорость с 5 до 10 км/ч, в чем вы без труда можете убедиться с помощью несложных вычислений.

Древние греки придумали множество парадоксов о времени и о движении Парадокс Зенона о бегуне («стадий») принадлежит к числу наиболее известных.

Бегун в парадоксе Зенона рассуждал следующим образом.

Бегун.Прежде чем я добегу до финиша, мне необходимо пробежать половину дистанции, затем половину оставшейся половины, то есть 3/4 всей дистанции.

Бегун.Прежде чем я преодолею последнюю четверть дистанции, мне необходимо пробежать ее половину. И так всякий раз. Прежде чем преодолеть какое-то расстояние, мне необходимо пробежать половину его. Этим половинам не будет конца! Я никогда не доберусь до финиша!

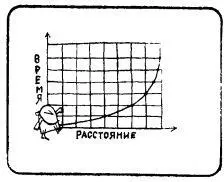
Предположим, что на преодоление половины каждого расстояния бегун затрачивает 1 мин. На графике зависимости времени от пути видно, что бегун приближается к финишу, но так и не достигает его. Правильны ли рассуждения бегуна?

Нет, неправильны: бегун не затрачивает по 1 мин на преодоление половины каждого отрезка. Каждую половину очередного отрезка он пробегает за вдвое меньшее время, чем половину предыдущего отрезка. Бегун достигнет финиша через 2 мин после старта, хотя ему придется за эти 2 мин преодолеть бесконечно много половин соответствующих отрезков дистанции.

Зенону принадлежит и другой, не менее знаменитый парадокс об Ахилле и черепахе. Быстроногий Ахилл хочет поймать черепаху, которая находится на расстоянии 1 км от него.

К тому времени, когда Ахилл добегает до того места, где первоначально находилась черепаха, та успевает уползти вперед на 10 м.