Поскольку все содержание работ А. А. Власова [1–5], относящееся к исследованию нестационарного случая, сводится к анализу несуществующего «дисперсионного уравнения», ясно, что его выводы, касающиеся «вибрационных свойств» и «недиссипативных потоков и их спонтанного возникновения в газе», появляются лишь в результате указанных грубых ошибок.
Таким образом, сделанное в начале статьи утверждение об отсутствии в разобранных работах А. А. Власова [1–5] каких-либо положительных результатов представляется нам доказанным.
Литература
1. Власов А. А. // J. Phys. 1946. 9. P. 26.
2. Власов А. А. // J. Phys. 1946. 9. P. 190.
3. Власов А. А. // Известия АН СССР. Сер. физика. 1944. 8, P. 248.
4. Власов А. А. // Ученые записки МГУ. 1945. № 77. С. 3.
5. Власов А. А. // ЖЭТФ. 1945. 15. С. 291.
6. Ландау Л. Д. // ЖЭТФ. 1946. 16. С. 574; Journ. of Phys. 1946. P. 25.
К обобщенной теории плазмы и теории твердого тела [47] Настоящая статья печатается как дискуссионная. — Ред.
Профессор А. А. Власов
Вестник Московского университета. Физика. Астрономия. 1946. № 3–4. Сокращенный текст
Коллективные взаимодействия, далекие пространственно-временные связи, процессы, не укладывающиеся в обычные рамки задачи Коши. (Ответ В. Гинзбургу, Л. Ландау, М. Леонтовичу, В. Фоку [48] См. ЖЭТФ. 1946. 16 , № 3 и № 7 (в дальнейшем цитируется как [К]).
.)
1. Новое уравнение
2. Проблема обоснования
3. Особенности метода «самосогласованного поля»: а) отличие от «обычных» методов, б) непосредственная связь между «микро» и «макро»
4. Неборновский кристалл: а) низкие температуры, б) высокие температуры, в) промежуточные температуры
5. Задача Коши, ее решения, особенности и следствия
6. Теория нового типа временных физических процессов, не укладывающихся в рамки задачи Коши
7. Заключение
1. Новое уравнение
В статьях [1–3] для понимания физических процессов в системах, состоящих из многих частиц, было предложено новое уравнение.
Объединяя результат статей [1] и [2] и делая дальнейший шаг (добавляя определенное число нелинейных функционалов), запишем здесь уравнение для системы N одинаковых частиц, взаимодействующих электродинамически, а также одновременно с произвольным центральным законом сил взаимодействия:
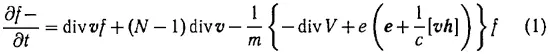
(уравнение непрерывности в пространстве шести измерений);
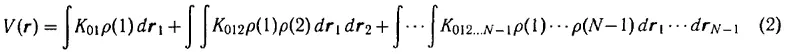
(ряд Тейлора-Вольтерра [4] для функционалов, оборванный на ( N—1 ) — м члене), где — f ( x,y,z,ξ,η,ς,t ) функция распределения для какой-либо одной частицы ансамбля, нормированная на единицу; ядра K 01, K 02, … зависят только от модуля расстояний между частицами, включают общее число частиц N :
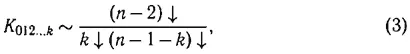
в остальном произвольны; ρ — вероятность местоположения частицы (плотность):
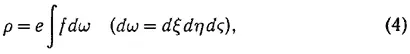
e и h — напряженности электрического и магнитного полей, связанных с функцией распределения через посредство зарядов и токов:
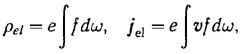
входящих в уравнения поля [1]:
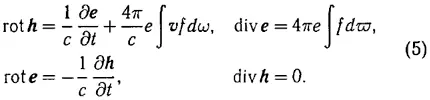
[Опущена часть, несущественная для рассмотрения.]
Система уравнений (5) представляет в сущности метод описания динамических свойств сред. Эти уравнения принципиально отличаются от схемы Больцмана интегральным учетом взаимодействий между частицами и отсутствием членов с «соударениями».
Метод существенно отличается от усредненных уравнений электромагнитного поля, в которых заложена предпосылка о разделении частиц на «свободные» и «связанные». Эта предпосылка радикальна — она обусловливает введение векторов поляризации и намагничивания, гарантирующих введение констант: диэлектрической постоянной и магнитной проницаемости. Излагаемый метод относится к другому крайнему случаю, где экспериментальные средства таковы, что не гарантируют строгой пространственной локализации отдельных частиц ансамбля у некоторых других.
Читать дальше

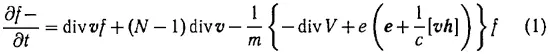
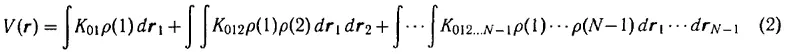
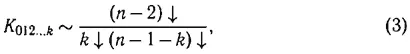
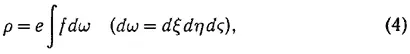
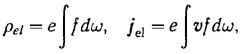
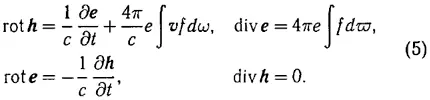



![Коллектив авторов Биографии и мемуары - Ковалиная книга. Вспоминая Юрия Коваля [второе издание, исправленное и дополненное]](/books/430445/kollektiv-avtorov-biografii-i-memuary-kovalinaya-kn-thumb.webp)






