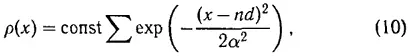
причем средний квадрат смещения частиц из положения равновесия равен

и одинаков для всех внутренних узлов цепочки. Из этой формулы, существенно отличающейся от выражения, вытекающего из классической статистики, виден также тот основной порок метода «самосогласованного поля», который и показывает его заведомую неприменимость к этим вопросам. Дело в том, что, как вытекает из вывода выражения (11), в сумме ∑ K ( nd ) присутствует член, соответствующий n = 0 .
Таким образом, формулы (10) и (11) показывают, что распределение плотности существенно зависит K'' (0) — от характера закона взаимодействия при бесконечно малом расстоянии между частицами, что нелепо само по себе. Заметим, что при нашем выводе мы молчаливо предполагали, что четная функция K(x) (где —∞ < x < +∞) непрерывна вместе со своими производными первого и второго порядка при x = 0. При этом предположении K'' (0) = 0 и (9) совпадает с (3), но K'' (0), очевидно, может и не быть нулем. Если же K ( x ) вблизи точки x = 0 — не аналитическая функция, то результат будет опять существенно зависеть от ее поведения в этой области, т. е. указанное нелепое следствие теории остается и в этом случае.
Указанный порок метода самосогласованного поля, как легко видеть, не связан с частными свойствами рассмотренного решения; еще до интегрирования видно, что поведение K ( x ) при x = 0 может играть существенную роль.
Добавим еще, что если в (1) K ( r ) заменить на K ( r )exp( K ( r ) /kT ) (так пытается усовершенствовать свое уравнение А. А. Власов в конце работы [2]), то, хотя ход дискуссии изложенного нами вопроса и ее результаты и изменяется, но при этом возникнут новые трудности и новые противоречия с результатами классической статистики.
Исходя из разобранных выше посылок А. А. Власов приходит к ряду выводов, относящихся к теории кристаллического состояния. Один из этих выводов, касающийся «наличия кристаллической структуры и ее спонтанного возникновения» [1, § 10; 3, § 9] мы и разберем здесь, так как он приводит автора к далеко идущим утверждениям. Именно на основании этого вывода он говорит о «новой теории кристаллического состояния, совершенно отличной от теории М. Борна, в которой позиция каждого атома фиксирована около положения равновесия» [1, с. 40].
Решая уравнение, получающееся из (1) с помощью линеаризации, автор приходит к выводу, что у последнего при известных условиях имеются периодические решения. Эту периодичность, как это особенно четко сформулировано им в начале § 9 статьи [3], он истолковывает как наличие кристаллической структуры. Период ее определяется уравнением (УШ) работы [2], которое при использовании формулы (8) той же работы принимает вид
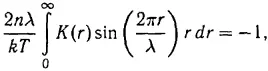
где λ — период структуры. Согласно этой формуле, период λ является функцией не только концентрации атомов N , но и температуры T . Однако это, очевидно, невозможно, поскольку среднее число частиц N в единице объема задано. Период простой решетки равен N - 1/3 (или при сложной структуре ячейки отличается от этой величины множителем) и явно от температуры все зависит.
Тот факт, что интерпретация решений уравнения (1) в этом случае приводит автора к таким странным следствиям, не должен нас удивлять, так как этот случай лежит вне границ физической применимости используемого уравнения.
2. Выше мы разбирали вопросы, связанные с теорией твердого тела. Помимо этого А. А. Власов в указанных работах (см. в особенности [1]) рассматривает нестационарные явления в многоатомных системах. Исходной здесь служит система уравнений (11) из работы [2], причем член дf/дt полагается равным нулю и проводится линеаризация, т. е. решение пишется в виде f = f 0+ ф , где ф<0. В результате получается следующее уравнение (3) в [3]):
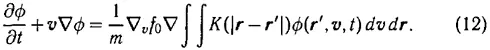
Автор ищет решение этого уравнения в виде
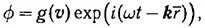
Читать дальше

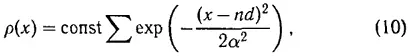

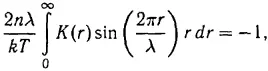
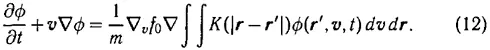
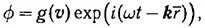



![Коллектив авторов Биографии и мемуары - Ковалиная книга. Вспоминая Юрия Коваля [второе издание, исправленное и дополненное]](/books/430445/kollektiv-avtorov-biografii-i-memuary-kovalinaya-kn-thumb.webp)






