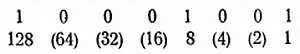Яков Перельман - Занимательная арифметика [Загадки и диковинки в мире чисел]

Вы всматриваетесь в эту фигуру и безошибочно называете задуманное число: 137.

Как вы узнаете его?

Способ станет ясен сам собой, если в выбранном примере (137) последовательно обозначить возле каждой спички то число, при делении которого она была положена (см. рисунок).

Секрет фокуса: что делает отгадчик.

Теперь понятно, что последняя спичка во всех случаях означает число 1, и не составляет труда, восходя от нее к предшествующим делениям, добраться до первоначально задуманного числа. Например, по фигуре рисунка вы можете вычислить, что задумано было число 664. В самом деле, выполняя последовательно удвоения (начиная с конца) и не забывая прибавлять, где надо, единицу, получаем задуманное (см. рисунок).

Какое число здесь изображено?

Таким образом, пользуясь спичками, вы прослеживаете ход чужих мыслей, восстанавливаете всю цепь выкладок.

Тот же результат мы можем получить иначе, сообразив, что лежащая спичка должна соответствовать в двоичной системе нолю (деление на 2 без остатка), а стоящая — единице.

Ответ на вопрос предыдущего рисунка.

Таким образом, в первом примере мы имеем (читая справа налево) число:

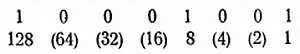
или в десятичной системе:

128 + 8 + 1 = 137.

А во втором примере задуманное число изображается по двоичной системе так:

или по десятичной системе:

512 + 128 + 16 + 8 = 664.

Попробуйте решить, какое число задумано, если получилась фигура рисунка на стр. 107.

Решение будет такое.

Число "10010101" в двоичной системе соответствует в десятичной:

128 + 16 + 4 + 1 = 149.

Необходимо заметить, что получаемая при последнем делении единица также должна быть отмечаема стоящей спичкой.

Какое число изображено этой фигурой?

У некоторых читателей, вероятно, возник уже вопрос, почему для выполнения описанных раньше опытов мы пользуемся именно двоичной системой? Ведь каждое число можно изобразить в любой системе, между прочим и в десятичной. Чем же объясняется предпочтение здесь двоичной?

Объясняется оно тем, что в этой системе, кроме ноля, употребляется всего одна цифра — единица, а следовательно, число составляется из различных степеней 2, взятых только по одному разу. Если бы в фокусе с кошельками мы распределили деньги, например, по пятеричной системе, то могли бы составить, не раскрывая кошельков, любую сумму лишь в том случае, когда каждый из кошельков повторялся бы у нас не менее 4 раз (в пятеричной системе употребляются ведь, кроме ноля, четыре цифры).

Впрочем, бывают случаи, когда для подобных надобностей удобнее пользоваться не двоичной, а троичной системой, несколько видоизмененной. Сюда относится знаменитая старинная "задача о гирях", которая может послужить сюжетом и для арифметического фокуса.

Представьте, что вам предложили придумать набор из четырех гирь, с помощью которых возможно было бы отвесить любое целое число килограммов, от 1 до 40. Двоичная система подсказывает вам набор:

1 кг, 2 кг, 4 кг, 8 кг, 16 кг,

которым можно отвешивать все грузы от 1 до 31 кг. Но это, очевидно, не удовлетворяет требуемым условиям ни по числу гирь, ни по предельному грузу (31 кг вместо 40). С другой стороны, вы не использовали здесь возможности класть гири не только на одну чашку весов, но и на две, то-есть обходиться не только суммой гирь, но и их разностью . Последнее дает так много разнообразных комбинаций, что вы совершенно теряетесь в поисках, не умея уложить их в какую-либо систему.

Если вам не посчастливится напасть на правильный путь, вы готовы будете даже сомневаться вообще в разрешимости задачи столь малым числом гирь, как четыре.

Посвященный выходит из этого затруднения с волшебной простотой, намечая следующие четыре гири:

1 кг, 3 кг, 9 кг, 27 кг.

Любое целое число килограммов, до 40 кг, вы можете отвесить такими гирями, кладя их то на одну, то на обе чашки весов. Не приводим примеров, потому что каждый легко может сам убедиться в полной пригодности такого набора гирь для нашей цели. Остановимся лучше на том, почему именно указанный ряд обладает этим свойством. Вероятно, читатели уже заметили, что числа эти — ряд степеней [33] Единицу можно рассматривать как нулевую степень 3 (вообще — как нулевую степень любого числа). числа 3: