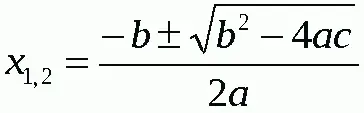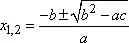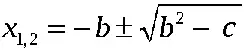W Cat - Система Диофанта

= Так, что надеясь на удачу выбирать случайное число.

— Не будем вручать удачу случаю. Действуй так в качестве запроса выбирай середину исследуемого диапазона и при каждой итерации этот диапазон будет в два раза уменьшаться. Попробуем сначала?

= 1. Не совсем понял, но 50.

— Задуманное меньше.

= 2. 25?

— Задуманное больше.

= 3. Догадался, остался диапазон от 49 до 26. Тогда 38?

— Задуманное больше.

= 4. 44?

— Задуманное меньше.

= 5. 41?

— Задуманное больше. Надеюсь ты все понял, и следующим вопросом выиграешь.

= "Ацнун цванцих.." [Главное, системный подход] - подумал принц целуя тысяча двадцать третью лягушку.

— Завтра организуй в классе соревнование по скорости угадывания. Не гарантирую 100% выигрыш, но в большинстве случаев — сработает.

— Но вернемся к тренировке:

x 2— 1,6x + 0,63 = 0

1. [4* 0,63 — 1,6 2= -0,04] — Дотрицателен

2. [ - + ] - оба корня положительны

3. [ 0,63 ] делители искать не будем.

4. [x 0= 0,8] меньший корень лежит в диапазоне от 0 до 0,8

. . . . 1. x 1= 0,4 x 2= 1,6 — 0,4 = 1,2 0,4*1,2=0,48

да, тяжелый случай; 0,48 < 0,63 и это значит, что корни взяты слишком далеко от x 0

. . . . 2. x 1= 0,6 x 2= 1,6 — 0,6 = 1 0,6*1=0,6

0,6 < 0,63 обнадеживает, что мы идем правильным путем.

. . . . 3. x 1= 0,7 x 2= 1,6 — 0,7 = 0,9 0,9*0,7=0,63

Дело сделано! В уме такое решить затруднительно, но тренируйся.

— Так дело не пойдет. Не готовы мы еще решать ЛЮБЫЕ задачи, а значит опять подготовим НАШИКУ

изменяем функцию генерации числа

4 | def gen_number(k):

5 | . . prime_number =(1, 2, 3, 5, 7, 11, 13, 17)

6 | . . sign_number =(0, 1, 2, 3)

7 | . . nu = prime_number[random.randint(0, k)]

8 | . . sign = random.choice(sign_number)

9 | . . if sign == 0:

10 | . . . . nu = nu * -1

11 | . . nu = nu + 0.1 * random.randint(0, 9)

12 | . . return nu

опять распечатываем полученные файлы и поражаем одноклассников (после солидной тренировки)

= Попробуем?

— x 2- 6.3x + 9.9 = 0

1. т.к. формула сгенерирована из подготовленных чисел решение гарантированно есть.

2. [ - + ] - оба корня положительны

3. т.к. КУ сделано с дробями то делители искать не будем.

4. [x 0= 3,15] меньший корень лежит в диапазоне от 0 до 3,15

. . . . 1. x 1= 1,3 x 2= 6,3 — 1,3 = 5 5*1,3=6,5

Маловато будет... И так далее. Но я то знаю ответ x 1= 3 x 2= 3,3

x 2- 10.09x - 112.493 = 0

x 2- 15.14x + 57.232 = 0

x 2- 22.78x + 92.644 = 0

x 2+ 4.49x - 87.986 = 0

x 2+ 15.36x + 36.704 = 0

x 2- 6.4x + 5.4 = 0 слабо, увидеть корни без решения

. . . . .

= Хе, хе, хе. Зря ты не хочешь посмотреть формулу корней квадратного уравнения

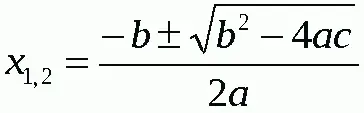
= Смотри: x 1,2= -b/2 ± z ничего не напоминает?

/ странно было бы если бы не напоминало/

- О! Давай развлечемся! Так, "a" как и положено будет равно 1. Подставляй в нужном виде i и j. Нет, никакой бумаги, все в уме. И далее... волшебное превращение квадрата суммы в квадрат разности; затем в простую разность, знакопеременно сражающуюся с суммой и после упрощения останется последний герой.

= Как интересно. Прямо триллер.

- Естественно. Математика чрезвычайно эмоциональное занятие.

- Но, давай прощаться. У тебя есть ТРИ метода поиска корней и в зависимости от ситуации ты выберешь самый эффективный.

= У нас в классе этим уже особо не удивишь. Пожалуй, пойду заниматься с сестренкой ей в следующем году найдется кого удивить мгновенными решениями.

— Заодно почитай с ней Яков Исидорович Перельман «Быстрый счет [Тридцать простых приемов устного счета]», да и остальные книги Перельмана очень и очень достойны внимания. Если хочешь, открой более современную Билл Хэндли «Считайте в уме как компьютер».

= Ну, ладно, пока.

Вот такие дела.

- Привет.

= Привет ?

Шо опять!!!

- Как ты знаешь, последние годы я развлекаюсь изготовлением fb2-версий книг. Последняя моя работа «Энциклопедический словарь юного математика» 1989 года издания (ясно, что статьи этой книги написаны намного раньше) несколько забавна здесь статья о вычислительной технике, ну что поделать, развитие стремительно (по закону Мура), а в остальном... математика штука стабильная, хотя... К недостаткам можно отнести, то, что упор в рассказе сделан на советских математиках, т.е. «за бортом» оказались... Но в целом, очень и очень интересно, в том числе и о КУ.

= Щас спою.

- Так вот. Если в КУ ax 2+ bx + c = 0 коэффициент b — четенТО изменяем запись ax 2+ 2 bx + c = 0 (т.е. bтеперь в два раза меньше) то корни будут:

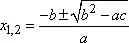
Но, если в нашем случае, a = 1, то:

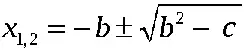
= Да! Существенные сокращения вычислений!