Эндрю Уэзеролл - Компьютерные сети. 5-е издание

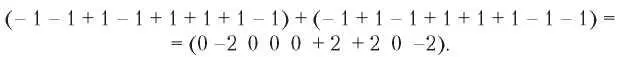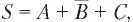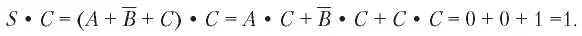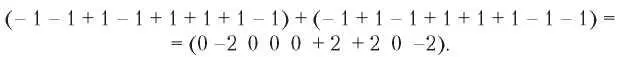
(- 1 - 1 + 1 - 1 + 1 + 1 + 1 - 1) + (- 1 + 1 - 1 + 1 + 1 + 1 - 1 - 1) =

= (0 -2 000 + 2 + 2 0 -2).

Чтобы восстановить исходный битовый поток каждой из станций, приемник должен заранее знать элементарные последовательности всех передатчиков, с которыми он работает. Восстановление осуществляется путем вычисления нормированного скалярного произведения принятой последовательности (то есть линейной суммы сигналов всех станций) и элементарной последовательности той станции, чей исходный сигнал восстанавливается. Если принята элементарная последовательность S и приемник пытается понять, что передала станция с элементарной последовательностью C , то производится вычисление нормированного скалярного произведения S • C.

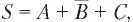
Чтобы понять, как это все работает, давайте представим себе эти две станции, A и C. Пусть обе передают единичный бит в то время, как станция B передает нулевой бит. Приемник получает сумму сигналов, которая равна: S = A + B + C, и вычисляет произведение:

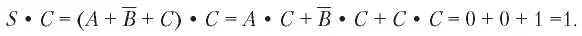
S • C = (A + B + C) • C = A • C + B • C + C • C = 0 + 0 + 1 =1.

Первые два слагаемых равны нулю, потому что все пары элементарных последовательностей тщательно подбирались такими, чтобы они были ортогональными, см. выражение (2.3). Теперь понятно, почему это условие должно быть наложено на элементарные последовательности.

Обратимся снова к шести примерам, показанным на рис. 2.24, в. Конкретный результат декодирования этих последовательностей представлен на рис. 2.24, г. Допустим, приемник заинтересован в извлечении потока битов, посланного станцией C , из всех шести последовательностей S 1-S 6. Для этого он вычисляет каждый бит путем суммирования парных произведений принятой последовательности ( S ) и вектора C (см. рис. 2.24, б), затем деления результата на 8 (так как m = 8 в данном случае). Как видите, каждый раз находится верный бит. Это так же просто, как говорить по-французски!

В идеальной системе CDMA без учета шумов, которую мы здесь изучили, допустимое количество станций, которые передают сигналы одновременно, может быть сколь угодно большим, при этом будут использоваться более длинные последовательности чипов. Для 2 п станции коды Уолша могут обеспечить 2 п ортогональных последовательностей длины 2 п. Однако имеется одно существенное ограничение — то, что мы предположили, что все чипы синхронизированы по времени в приемнике. Эта синхронизация даже приближенно не выполняется в таких приложениях, как сотовая связь (где CDMA был широко внедрен начиная с 1990-х).

Мы вернемся к этой теме позже и опишем, чем асинхронный CDMA отличается от синхронного CDMA.

Кроме сотовой связи CDMA используется спутниками и кабельными сетями. Мы в нашем кратком представлении пропустили много усложняющих факторов. Инженеры, которые хотят получить глубокое понимание CDMA, должны читать Viterbi (1995) и Lee and Miller (1998). Чтение этих материалов, впрочем, требует довольно мало знаний в коммуникационной инженерии.

2.6. Коммутируемая телефонная сеть общего пользования

Когда между двумя компьютерами, принадлежащими одной компании и расположенными недалеко друг от друга, необходимо установить связь, часто проще всего оказывается проложить между ними кабель. Подобным образом работают локальные сети. Однако, когда расстояния велики, или компьютеров очень много, или кабель надо прокладывать поперек шоссе или еще какой-либо государственной магистрали, цена прямого кабельного соединения становится недоступно высокой. Кроме того, почти во всех странах мира законом запрещено протягивать частные линии связи над или под объектами государственной собственности. Поэтому проектировщики сетей должны рассчитывать на имеющиеся средства телекоммуникации.

Подобные средства связи, в частности коммутируемая телефонная сеть общего пользования(PSTN, Public Switched Telephone Network), были созданы много лет назад с совершенно иной целью — передать человеческий голос в более-менее узнаваемом виде. Их применимость для соединения друг с другом компьютеров весьма незначительна.

Чтобы увидеть размер проблемы, предположим, что дешевый потребительский кабель, работающий между двумя компьютерами, может передать данные со скоростью 1 Гбит/с или больше. При этом типичный ADSL, прекрасная быстрая альтернатива телефонному модему, работает в пределах 1 Мбит/с. Это различие — как различие между полетом на самолете и неторопливой прогулкой.