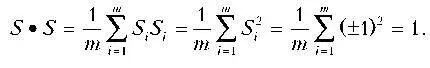Эндрю Уэзеролл - Компьютерные сети. 5-е издание

Чтобы передать один бит, станция посылает свою элементарную последовательность. Чтобы передать бит со значением 0, нужно отправить вместо элементарной последовательности ее дополнение (все единицы последовательности меняются на нули, а все нули — на единицы). Никакие другие комбинации передавать не разрешается. Таким образом, если m = 8 и если станции A соответствует последовательность (-1 -1 -1 +1 +1 -1 +1 +1), она может послать бит «1», передав элементарную последовательность, а бит «0», передав (+1 +1 +1 -1 -1 +1 -1 -1). Здесь посылаются настоящие сигналы с такими уровнями напряжения, но нам достаточно думать о них как о последовательностях чисел.

Увеличить количество информации, которое необходимо передавать (чтобы скорость составила b бит/с, нужно отправлять mb элементарных сигналов в секунду), можно только за счет увеличения в m раз пропускной способности. Таким образом, для CDMA нужна в m раз большая пропускная способность, чем для станции не

применяющей CDMA (предполагая, что никаких изменений в методах модуляции и кодирования не производилось). Если имеется полоса шириной 1 МГц, на которой работают 100 станций, то при частотном уплотнении каждая из них получила бы свои 10 кГц и работала бы со скоростью 10 Кбит/с (предположим, используется 1 бит/Гц). При CDMA каждая станция использует всю ширину диапазона (1 МГц), так что скорость передачи элементарных сигналов достигает сотни и «размазывает» пропускную способность станции 10 Кбит/с на все каналы.

На рис. 2.24, а и б мы покажем элементарные последовательности четырех станций и сигналы, которыми они представляются.

Каждая станция имеет собственную уникальную элементарную последовательность. Обозначим символом S вектор длины m для станции S, а символом S — дополнение S. Все элементарные последовательности попарно ортогональны. Мы имеем в виду, что нормированное скалярное произведение двух различных элементарных последовательностей S и T (пишется S • T ) равно 0. Известно, как генерировать такие последовательности с помощью метода, известного как коды Уолша. Используя математическую запись, можно выразить вышесказанное таким образом:

Попросту говоря, сколько всего пар, столько и разных пар. Это свойство ортогональности мы строго докажем чуть позже. Обратите внимание: если S • T = 0, то и S • T также равно 0. Нормированное скалярное произведение любой элементарной последовательности на саму себя равно 1:

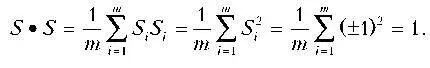
Это действительно так, поскольку каждое из m слагаемых суммы равно 1, поэтому вся сумма равна m. Обратите также внимание на то, что S • S = -1.

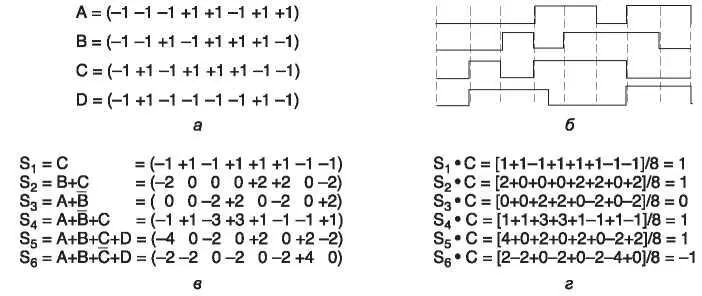
Рис. 2.24.Последовательность: а — двоичные элементарные последовательности для четырех станций; б — биполярные элементарные двоичные последовательности; в — шесть примеров передачи; г — восстановление сигнала станции C

В течение каждого битового интервала станция может либо передавать 1, посылая свою элементарную последовательность, либо передавать 0, посылая дополнение к последовательности, либо может молчать и ничего не передавать. Предположим, что все станции синхронизировались во времени, то есть все последовательности начали передаваться в один и тот же момент.

Когда две или более станции пытаются осуществить одновременную передачу, их биполярные сигналы линейно складываются. Например, если при передаче одного элементарного сигнала три станции послали +1, а одна послала -1, то в результате получится +2. Можно рассматривать это как сложение напряжений: три станции имеют на выходе +1 В, а одна имеет на выходе -1 В. В результате сложения получаем +2 В.

На рис. 2.24, в изображено шесть примеров передачи, в которой одновременно принимают участие одна или несколько станций. В первом примере С передает единичный бит, поэтому мы просто получаем элементарную последовательность этой станции. Во втором примере и B и C передают единичные биты, в результате чего мы получаем сумму их биполярных последовательностей, а именно: