2.1. Теоретические основы передачи данных
Информация может передаваться по проводам за счет изменения какой-либо физической величины, например напряжения или силы тока. Представив значение напряжения или силы тока в виде однозначной функции времени, f(t), мы сможем смоделировать поведение сигнала и подвергнуть его математическому анализу. Этому анализу и посвящены следующие разделы.
2.1.1. Ряды Фурье

2.1.2. Сигналы с ограниченным спектром
Вы спросите, какое отношение все это имеет к передаче данных? В зависимости от физических характеристик каналов сигналы с разными частотами ведут себя в них по-разному. Рассмотрим конкретный пример — передачу двоичного кода ASCII символа «b». Для этого потребуется 8 бит (то есть 1 байт). Задача — передать следующую последовательность бит: 01100010. На рис. 2.1, а слева изображена зависимость выходного напряжения от времени на передающем компьютере. В результате анализа Фурье для данного сигнала получаем следующие значения коэффициентов:
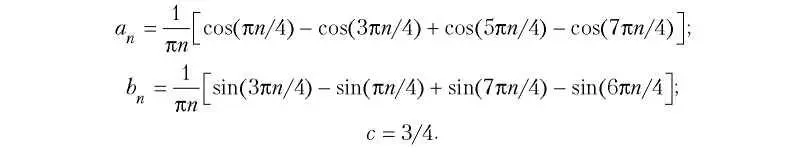
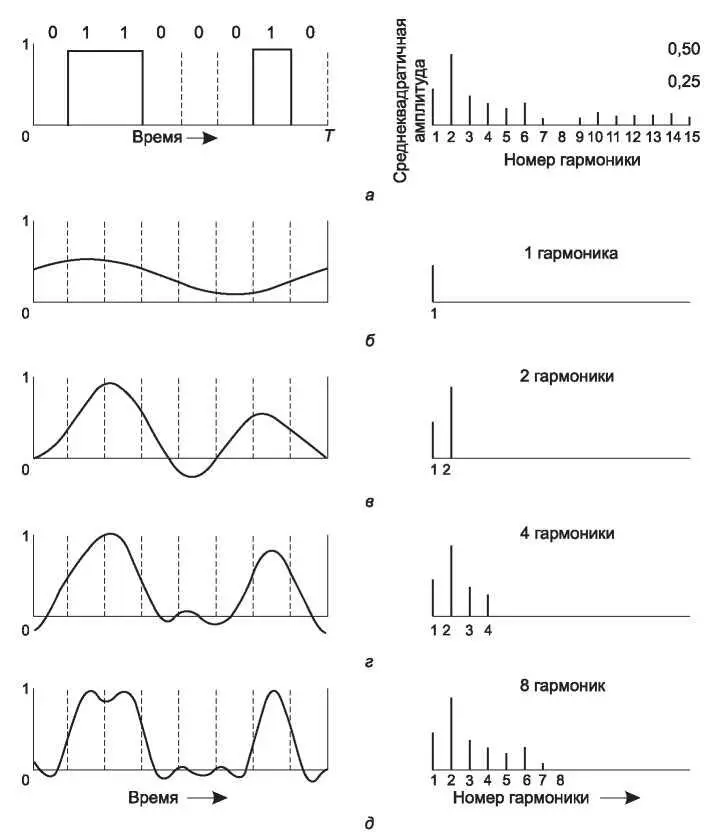
Рис. 2.1.Двоичный сигнал и его среднеквадратичные гармоники Фурье (а); последовательные приближения к оригинальному сигналу (б-д)
Среднеквадратичные амплитуды, 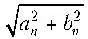 , для нескольких первых гармоник пока
, для нескольких первых гармоник пока
заны на рис. 2.1, а справа. Эти значения представляют интерес, поскольку их квадраты пропорциональны энергии, передаваемой на соответствующей частоте.
Ни один канал связи не может передавать сигналы без потери мощности. Если бы все гармоники ряда Фурье уменьшались при передаче в равной степени, то сигнал уменьшался бы по амплитуде, но не искажался (то есть у него была бы та же самая замечательная прямоугольная форма, как на рис. 2.1, а). К сожалению, все каналы связи уменьшают гармоники ряда Фурье в разной степени, тем самым искажая передаваемый сигнал. Как правило, по кабельным сетям амплитуды передаются почти без уменьшения в частотном диапазоне от 0 до некоей частоты 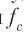 (измеряемой в периодах
(измеряемой в периодах
в секунду или герцах (Гц)), при этом высокочастотная составляющая сигнала (выше частоты f c, называемой частотой среза) заметно ослабляется. Этот диапазон частот называется полосой пропускания. На практике срез вовсе не является таким резким, поэтому обычно в упомянутую выше полосу пропускания включают те частоты, которые передаются с потерей мощности, не превышающей 50 %.
Полоса пропускания является физической характеристикой среды передачи данных и зависит, например, от конструкции, толщины и длины носителя — провода или оптоволокна. Иногда для намеренного уменьшения полосы пропускания, доступной абонентам, в линию включается специальное устройство — фильтр. Например, беспроводным каналам стандартов 802.11 выделяется полоса пропускания шириной примерно 20 МГц, поэтому радиопередатчики соответствующим образом урезают сигнал. Еще один пример: у традиционных (аналоговых) телевизионных каналов полоса пропускания равна 6 МГц, независимо от того, передаются данные по проводам или беспроводным способом. Благодаря такой фильтрации в определенном диапазоне спектра можно передать большее количество сигналов, за счет чего повышается общая эффективность системы. Диапазон частот отдельных сигналов будет начинаться со значения, отличного от нуля, но это не играет никакой роли. Полоса пропускания — это все также некий разрешенный диапазон частот, и возможность передачи информации зависит только от его ширины, но не от начального и конечного значения частот. Сигналы, передающиеся в диапазоне частот от 0 и до верхней границы полосы, называются модулирующими сигналами. Сигналы, которые сдвигаются в верхний диапазон частот, как, например, для всех видов беспроводной передачи данных, называются сигналами в полосе.
Теперь посмотрим, как будет выглядеть сигнал, изображенный на рис. 2.1, а, если полоса пропускания канала будет такой, что через него будут проходить только самые низкие частоты (то есть функция g(t) будет аппроксимирована лишь несколькими первыми членами рядов выражения (2.1)). На рис. 2.1, б показан сигнал на выходе канала, пропускающего лишь первую (основную, f ) гармонику сигнала. Аналогично, рис. 2.1, в-д показывают спектры и восстановленные сигналы для каналов с более широкой полосой пропускания. Что касается цифровых данных, то главная задача — передавать их с минимальным качеством, позволяющим восстановить первоначальную последовательность битов. Для этого достаточно сигнала, показанного на рис. 2.1, д; следовательно, совершенно не нужно тратить ресурсы и использовать большее количество гармоник для получения более точной копии.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


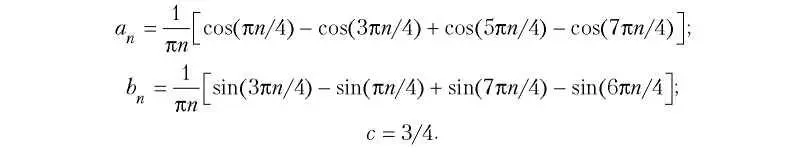

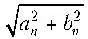 , для нескольких первых гармоник пока
, для нескольких первых гармоник пока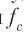 (измеряемой в периодах
(измеряемой в периодах







