Эндрю Уэзеролл - Компьютерные сети. 5-е издание

Вскоре после этого мост В1 получает эти кадры. Разумеется, он не знает (и не может знать), что это копии одного кадра, а не два разных кадра, посланных один за другим. Поэтому мост В2 отправляет копии кадра F 1во все свои порты. Так возникают F 3и F 4, которые по двум соединениям отправляются обратно в В1. Мост В1 видит два новых кадра с неизвестным адресом назначения и копирует их снова. Этот цикл продолжается вечно.

Решение данной проблемы заключается в установлении связи между мостами и наложении на реальную топологию сети связующего дерева (spanning tree), до-

стигающего каждого моста. В результате некоторые возможные соединения между мостами игнорируются с целью создания фиктивной бескольцевой топологии, которая является подмножеством реальной топологии.

Например, на рис. 4.41 показаны пять мостов, которые связаны и имеют соединенные с ними станции. Каждая станция соединяется только с одним мостом. Есть некоторые избыточные соединения между мостами, так что если будут использоваться все соединения, кадры будут отправлены в циклы.

Эта система может быть представлена в виде графа с мостами в качестве узлов и соединениеми между ними —в качестве ребер. Такой граф можно редуцировать до связующего дерева, которое по определению не имеет циклов, удалив из него соединения, изображенные на рис. 4.41 пунктирными линиями. В получившемся связующем дереве между каждыми двумя станциями существует только один путь. После того как мосты договорятся друг с другом о топологии связующего дерева, все коммуникации осуществляются только по ветвям этого дерева. Поскольку путь от отправителя к получателю единственный, зацикливание невозможно.

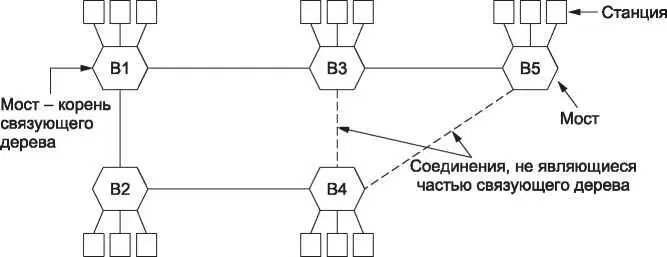
Рис. 4.41. Связующее дерево, соединяющее пять мостов. Пунктирными линиями показаны соединения, которые не входят в связующее дерево

Чтобы построить связующее дерево, мосты применяют следующий распределенный алгоритм. Каждый мост периодически рассылает по всем своим портам конфигурационное сообщение своим соседям и обрабатывает сообщения, полученные от других мостов, как описано ниже. Эти сообщения не передаются дальше, так как их цель — построение дерева, которое затем используется для пересылки.

Мосты должны сначала выбрать один мост, который будет корнем связующего дерева. Чтобы сделать этот выбор, каждый из них включает в конфигурационное сообщение идентификатор, основанный на своем MAC-адресе, так же как идентификатор моста, который он предполагает корнем. MAC-адреса установлены изготовителем и гарантировано уникальны во всем мире, что делает эти идентификаторы удобными и гарантированно разными. Мосты выбирают в качестве корня мост с наименьшим идентификатором. После обмена достаточным числом сообщений, чтобы распространить эту новость, все мосты договорятся, какой мост является корнем. На рис. 4.41 мост B1 имеет наименьший идентификатор и становится корнем.

Затем создается дерево кратчайших путей от корня до каждого моста. На рис. 4.41 мосты B2 и B3 могут быть достигнуты от моста B1 непосредственно, за один шаг, который является кратчайшим путем. Мост B4 может быть достигнут за два шага, или через B2 или через B3. Чтобы разрубить этот узел, выбирается путь через мост с наименьшим идентификатором, таким образом, B4 будет достигнут через B2. Мост B5 может быть достигнут за два шага через B3.

Чтобы найти эти кратчайшие пути, мосты включают в конфигурационные сообщения расстояние от корня. Каждый мост помнит кратчайший путь, который он находит к корню. Затем мосты отключают порты, которые не являются частью кратчайшего пути.

Хотя дерево охватывает все мосты, но не все соединения (или даже мосты) обязательно присутствуют в дереве. Это происходит, потому что отключение портов ликвидирует некоторые соединения в сети, чтобы предотвратить появление циклов. Алгоритм построения дерева продолжает работать постоянно, обнаруживая изменения в топологии и обновляя структуру дерева.

Автором распределенного алгоритма построения связующего дерева является Радья Перлман (Radia Perlman). Ее задачей было решить проблему объединения локальных сетей без циклов. Ей была дана неделя на решение этой задачи, но она придумала идею алгоритма связующего дерева за один день, так что у нее осталось время изложить ее в виде стихотворения (Perlman, 1985).

I think that I shall never see A graph more lovely than a tree.