Елисеев Д - Рассказы о математике с примерами на языках Python и C

Это последовательность “999999”, находящаяся на 762м знаке от начала. Желающие могут поэкспериментировать дальше самостоятельно с помощью программы на языке Python:

from math import factorial

from decimal import *

def chudnovsky(n):

pi = Decimal(0)

k = 0

while k < n:

pi += (Decimal(-1)**k)*(Decimal(factorial(6*k))/((factorial(k)**3)*(factorial(3*k)))* (13591409 + 545140134*k)/(640320**(3*k)))

k += 1

print("Шаг: {} из {}".format(k, n))

pi = pi * Decimal(10005).sqrt()/4270934400

pi = pi**(-1)

return pi

# Требуемая точность (число знаков)

N = 1000

getcontext().prec = N

val = chudnovsky(N/14)

print(val)

Эта программа не оптимизирована, и работает довольно-таки медленно, но для ознакомления с сутью алгоритма этого вполне достаточно. Кстати, с помощью формулы Чудновского два инженера Александр Йи и Сингеру Кондо в 2010 году объявили о новом мировом рекорде вычисления Пи на персональном компьютере: 5 трлн знаков после запятой. Компьютеру с 12 ядрами, 97Гб памяти и 19 жесткими дисками потребовалось 60 дней для выполнения расчетов.

На этом мы закончим с числом Пи, хотя с ним конечно, связано куда больше интересных фактов. Например 3 марта (т.е. 03.14) отмечается международный “день числа Пи”, ну а другие факты читатели могут поискать самостоятельно.

4. Вычисление радиуса Земли

О том, что Земля круглая сегодня знает каждый школьник, и никого не удивить таким видом планеты из космоса.

Однако в историческом плане, увидеть планету свысока мы смогли совсем-совсем недавно. Как же мог греческий ученый Эратосфен измерить радиус Земли, в 240 году до нашей эры? Оказывается мог, используя 2 научных “инструмента” - транспортир и верблюда, ну и разумеется, математику.

Эратосфен жил в Александрии - крупнейшем городе того времени, центром науки и искусств древнего мира. В Александрии по преданию, находился маяк высотой 120 метров - даже сегодня такое сооружение не просто построить, а в то время маяк считался одним из 7 чудес света. Эратосфен же был не только ученым, но и хранителем Александрийской библиотеки, содержащей до 700000 книг.

Читая труды по географии, Эратосфен нашел интересный факт - в городе Сиене в день летнего солнцестояния Солнце стоит так высоко, что предметы в полдень не отбрасывают тени. Другой может и не обратил бы на это внимание, но Эратосфен не зря интересовался и математикой и астрономией. Он знал что в его городе Александрии тень в этот же день имеет другой угол. Эратосфен дождался солнцестояния, измерил угол солнечных лучей и получил величину 7,2 градуса.

Что это значит? Объяснение данному факту могло быть только одно - Земля круглая, и угол падения солнечных лучей в разных точках Земли в одно время различается.

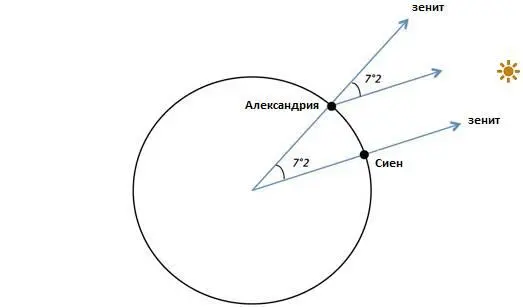
Картинка с сайта physicsforme.com

Дальше, как говорится, дело техники. Зная примерное расстояние между Сиеном и Александрией (которое было известно из времени в пути каравана верблюдов) и угол, легко получить длину всей окружности. К чести Эратосфена, его результат отличается от сегодняшнего всего лишь на 1%. Так, задолго до эпохи авиации и воздухоплавания, человек впервые смог измерить радиус планеты, даже при этом не отрываясь от нее. Увидеть настоящую кривизну Земли сумели лишь пилоты стратостатов в начале 20 века, более чем через 2000 лет после описанного опыта.

Разумеется, повторить подобный эксперимент сегодня легко может любой школьник. Нужно лишь сделать простейший угломер из транспортира и отвеса, и с помощью знакомых в другом городе, сделать измерения высоты Солнца в двух точках в одно и то же время.

5. Простые числа

Каждый знает, что простые числа — такие числа, которые делятся только на единицу и самих себя. Но так ли они просты, как кажутся, и актуальны ли сегодня? Попробуем разобраться.

То, что существуют числа, которые не делятся ни на какое другое число, люди знали еще в древности. Последовательность простых чисел имеет следующий вид:

1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61 …

Доказательство того, что этих чисел бесконечно много, дал еще Евклид, живший в 300 г до н.э. Примерно в те же годы уже известный нам греческий математик Эратосфен, придумал довольно-таки простой алгоритм получения простых чисел, суть которого была в последовательном вычеркивании чисел из таблицы. Те оставшиеся числа, которые ни на что не делились, и были простыми. Алгоритм называется «решето Эратосфена» и за счет своей простоты (в нем нет операций умножения или деления, только сложение) используется в компьютерной технике до сих пор.