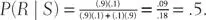9. Bayes’ Theorem allows us to answer the question “What is the probability a person is of a particular type (such as a performance enhancing steroid user) given that they say or do something in particular (such as test positive for steroids)?” To answer this question we must solve the following calculation: Let P stand for probability, R for being a steroid user, S for testing positive, and ˜R for being the type of baseball player who does not use steroids. The straight line symbol | is read as “given.” Then P(R | S) = 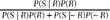 read as “the probability of being a steroid user given that you tested positive (P[R | S]) equals the probability of testing positive given that you are a steroid user times the probability of being a steroid user divided by that same quantity plus the probability of testing positive given that you are not a steroid user times the probability that you are not a steroid user.” Thus, the calculation is conditioned on the two sets of people who test positive: those who use steroids and those who don’t. In the baseball example this translates into
read as “the probability of being a steroid user given that you tested positive (P[R | S]) equals the probability of testing positive given that you are a steroid user times the probability of being a steroid user divided by that same quantity plus the probability of testing positive given that you are not a steroid user times the probability that you are not a steroid user.” Thus, the calculation is conditioned on the two sets of people who test positive: those who use steroids and those who don’t. In the baseball example this translates into 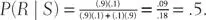
Chapter 3: Game Theory 102
1. The first major efforts to show that arms races lead to war are the work of Lewis Fry Richardson, a distinguished meteorologist who predicted World War I but, using the same logic, failed to anticipate World War II. See his Arms and Insecurity (Chicago: Quadrangle, 1960). The literature tying arms races to war is vast but almost universally fails to consider that arms purchases are anticipatory, or, in game-theory lingo, they are endogenous, strategic decisions.
2. The subject of renegotiation-proofness has attracted the interest of many economists, leading to a vast literature. Some seminal papers include Dilip Abreu, David Pearce, and Ennio Stacchetti, “Renegotiation and Symmetry in Repeated Games,” Journal of Economic Theory 60, no. 2 (1993): 217-40; Jean-Pierre Benoit and Vijay Krishna, “Renegotiation in Finitely Repeated Games,” Econometrica 61 (1993): 303-23; and James Bergin and W. Bentley MacLeod, “Efficiency and Renegotiation in Repeated Games,” Journal of Economic Theory 61, no. 1 (1993): 42-73.
3. The seminal work on this question dates back to the eighteenth-century French philosopher, mathematician, and nobleman the Marquis de Condorcet. Regrettably, the latter characteristic—he opposed beheading the king and queen—cost him his life during the French Revolution. There is a wonderful statue of him on the left bank of the Seine, not too far from Notre Dame. I always pay homage to him when I am in Paris. His insights were built upon in the second half of the twentieth century to establish the modern understanding of voting methods. See, for instance, Kenneth Arrow, Social Choice and Individual Values (New York: John Wiley and Sons, 1951); William H. Riker, Liberalism Against Populism (New York: Freeman, 1982); Richard D. McKelvey and Norman Schofield, “Structural Instability of the Core,” Journal of Mathematical Economics 15, no. 3 (June 1986): 179-98; and Gary W. Cox, Making Votes Count (New York: Cambridge University Press, 1997).
Chapter 4: Bombs Away
1. Stanley Feder, “Factions and Policon: New Ways to Analyze Politics,” in H. Bradford Westerfield, ed., Inside CIA’s Private World: Declassified Articles from the Agency’s Internal Journal, 1955—1992 (New Haven: Yale University Press, 1995).
2. This is a casual statement of the median voter theorem, one of the most important concepts in understanding issue resolutions. See Duncan Black, The Theory of Committees and Elections (Cambridge: Cambridge University Press, 1958), and Anthony Downs, An Economic Theory of Democracy (New York: Harper, 1957).
3. This second first-cut prediction relies on the mean voter theorem. See Andrew Caplin and Barry Nalebuff, “Aggregation and Social Choice: A Mean Voter Theorem,” Econometrica 59 (1991): 1-23; and Norman Schofield, “The Mean Voter Theorem: Necessary and Sufficient Conditions for Convergent Equilibrium,” Review of Economic Studies 74 (2007): 965-80.
4. See Bruce Bueno de Mesquita, “Ruminations on Challenges to Prediction with Rational Choice Models,” Rationality and Society 15, no. 1 (2003): 136-47; and Robert Thomson, Frans N. Stokman, and Christopher H. Achen, eds., The European Union Decides (Cambridge: Cambridge University Press, 2006).
Chapter 5: Napkins for Peace
1. For a not-too-technical explanation of what goes on inside the model, see Bruce Bueno de Mesquita, Predicting Politics (Columbus: Ohio State University Press, 2002).
2. Bruce Bueno de Mesquita, “Multilateral Negotiations: A Spatial Analysis of the Arab-Israeli Dispute,” International Organization (Summer 1990): 317-40.
3. See http://news.bbc.co.uk/1/hi/world/middle_east/1763912.stm.
4. Anthony H. Cordesman, The Israel-Palestinian War: Escalating to Nowhere (Westport, Conn.: Praeger, 2005): 219.
Chapter 6: Engineering the Future
1. For an early, foundational study applying war-of-attrition games, see John Maynard Smith and Geoffrey A. Parker, “The Logic of Asymmetric Contests,” Animal Behaviour 24 (1976): 159-75. See also Anatol Rapaport, Two Person Game Theory (Ann Arbor: University of Michigan Press, 1966).
2. See, for instance, James D. Fearon, “Rationalist Explanations for War,” International Organization 49 (1995): 379-414.
Chapter 7: Fast-Forward the Present
1. For a deeper exploration of some surprising implications of commitment problems and the pursuit of peace with adversaries, in particular peace with terrorists, see Ethan Bueno de Mesquita, “Conciliation, Counter-Terrorism, and Patterns of Terrorist Violence,” International Organization 59, no. 1 (2005): 145-76.
2. The actual calculation predicting the impact of deaths (the horizontal axis) on tourism (the vertical axis) is based on the logarithm of deaths to capture order-of-magnitude changes. Doubling the lives lost from 10 deaths to 20, for instance, represents a more noticeable change than going from 190 to 200 deaths even though the absolute change is the same. Logarithms capture the magnitude of change so that equal spaces reflect equal percentage increments in lost lives.
3. Limitations on the availability of data constrain the number of years I can cover. Violence and tourism are both measured quarterly. The Palestinians suffer the lion’s share of violent deaths. The graph looks very much the same if only Palestinian deaths are plotted rather than all violent deaths resulting from the conflict. Data on Israeli tourism are from the Bank of Israel and can be found at http://www.bankisrael.gov.il/series/en/catalog/tourism/tourist entries/. Data on violent deaths are from David Fielding, “How Does Violent Conflict Affect Investment Location Decisions?” Journal of Peace Research 41, no. 4 (2004): 465-84.
4. See “Palestinian Central Bureau of Statistics Press Release for the Hotel Survey, Fourth Quarter 2005,” found at www.pcbs.pna.org/Portals/_pcbs/PressRelease/HOTEL0405.pdf.
Chapter 8: How to Predict the Unpredictable
1. See John Lewis Gaddis, “International Relations Theory and the End of the Cold War,” International Security 17, no. 3 (Winter 1992): 323-73; and James Ray and Bruce Russett, “The Future as Arbiter of Theoretical Controversies: Predictions, Explanations and the End of the Cold War,” British Journal of Political Science 26, no. 4 (October 1996): 441-70.
Читать дальше

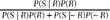 read as “the probability of being a steroid user given that you tested positive (P[R | S]) equals the probability of testing positive given that you are a steroid user times the probability of being a steroid user divided by that same quantity plus the probability of testing positive given that you are not a steroid user times the probability that you are not a steroid user.” Thus, the calculation is conditioned on the two sets of people who test positive: those who use steroids and those who don’t. In the baseball example this translates into
read as “the probability of being a steroid user given that you tested positive (P[R | S]) equals the probability of testing positive given that you are a steroid user times the probability of being a steroid user divided by that same quantity plus the probability of testing positive given that you are not a steroid user times the probability that you are not a steroid user.” Thus, the calculation is conditioned on the two sets of people who test positive: those who use steroids and those who don’t. In the baseball example this translates into