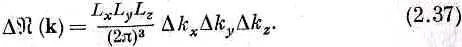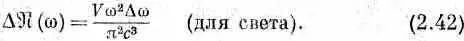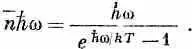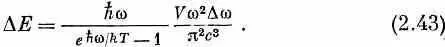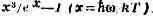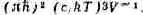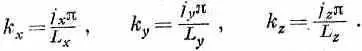
Число типов колебаний с k x в интервале D k x, как и прежде, равно
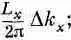
то же и с D k y, и с D k z. Если обозначить через 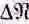 ( k) число таких типов колебаний, в которых векторное волновое число k обладает х-компонентой в интервале от k x до k x+D k x, у-компонентой в интервале от k y до k y+D k yи z-компонентой в интервале от k z до. k z+D k z, то
( k) число таких типов колебаний, в которых векторное волновое число k обладает х-компонентой в интервале от k x до k x+D k x, у-компонентой в интервале от k y до k y+D k yи z-компонентой в интервале от k z до. k z+D k z, то
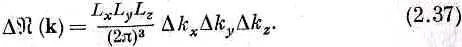
Произведение L x L y L z — это объем V ящика. Итак, мы пришли к важному результату, что для высоких частот (длин волн, меньших, чем габариты полости) число мод (типов колебаний) в полости пропорционально ее объему V и «объему в k -пространстве» D k хD k yD k z. Этот результат то и дело появляется то в одной, то в другой задаче, и его стоит запомнить:

Хоть мы этого и не доказали, результат не зависит от формы
ящика.
Теперь мы применим этот результат для того, чтобы найти число фотонных мод для фотонов с частотами в интервале Dw. Нас интересует всего-навсего энергия разных собственных колебаний, а не направления самих волн. Мы хотим знать число собственных колебаний в данном интервале частот. В вакууме величина kсвязана с частотой формулой
| k| =w/c. (2.39)
Значит, в интервал частот Dw попадают все моды, отвечающие векторам k, величина которых меняется от k до k +D k независимо от направления. «Объем в k-пространстве» между k и k +D k — это сферический слой, объем которого равен
4p k 2D k .
Количество собственных колебаний (мод) тогда равно

Однако раз нас интересуют частоты, то надо подставить k = w / c , и мы получаем

Но здесь возникает одно усложнение. Если мы говорим о собственных колебаниях электромагнитной волны, то каждому данному волновому вектору kможет соответствовать любая из двух поляризаций (перпендикулярных друг другу). Поскольку эти собственные колебания независимы, то нужно (для света) удвоить их число. И мы имеем
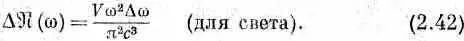
Мы показали уже [см. (2.33)], что каждое собственное колебание (мода, тип колебаний, «состояние») обладает в среднем
энергией
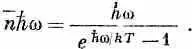
Умножая это на число собственных колебаний, мы получаем энергию D Е. которой обладают собственные колебания лежащие в интервале Dw
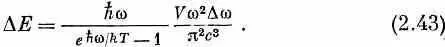
Это и есть закон для спектра частот излучения абсолютно черного тела, найденный нами уже однажды в гл. 41 (вып. 4). Спектр этот вычерчен на фиг. 2.10.
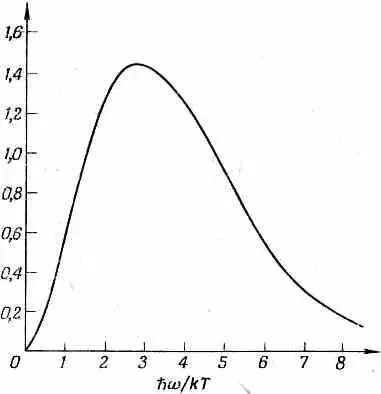
Фиг. 2.10. Спектр частот излучения в полости при тепловом равновесии (спектр «абсолютно черного тела»).
На оси ординат отложена величина 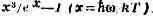
отличающаяся от d E / d w постоянным множителем 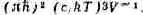
Вы теперь видите, что ответ зависит от того факта, что фотоны являются бозе-частицами — частицами, имеющими тенденцию собираться всем вместе в одном и том же состоянии (амплитуда такого поведения велика). Бы помните, что именно Планк, изучавший спектр абсолютно черного тела (который представлял загадку для классической физики) и открывший формулу (2.43), положил тем самым начало квантовой механике.
Читать дальше

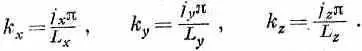
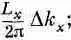
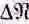 ( k) число таких типов колебаний, в которых векторное волновое число k обладает х-компонентой в интервале от k x до k x+D k x, у-компонентой в интервале от k y до k y+D k yи z-компонентой в интервале от k z до. k z+D k z, то
( k) число таких типов колебаний, в которых векторное волновое число k обладает х-компонентой в интервале от k x до k x+D k x, у-компонентой в интервале от k y до k y+D k yи z-компонентой в интервале от k z до. k z+D k z, то