Feynmann - Feynmann 8

(п+1)| a | 2, (2.28)

а вероятность того, что он фотон поглотит, равна

n | а | 2, (2.29)

где | а | 2— вероятность того, что он испустил бы фотон, если бы не было этих n фотонов. Мы уже говорили об этих правилах немного по-иному в гл. 42 (вып. 4). Выражение (2.29) утверждает, что вероятность того, что атом поглотит фотон и совершит переход в состояние с более высокой энергией, пропорциональ­на интенсивности света, освещающего его. Но, как впервые указал Эйнштейн, скорость, с которой атом переходит в более низкое энергетическое состояние, состоит из двух частей. Есть вероятность | а| 2того, что он совершит самопроизвольный переход, и есть вероятность вынужденного перехода n |а| 2 , пропорциональная интенсивности света, т. е. числу имеющихся фотонов. Далее, как заметил Эйнштейн, коэффициенты погло­щения и вынужденного испускания равны между собой и свя­заны с вероятностью самопроизвольного испускания. Здесь же мы выяснили, что если интенсивность света измеряется ко­личеством имеющихся фотонов (вместо того, чтобы пользоваться энергией в единице объема или в секунду), то коэффициенты поглощения, вынужденного испускания и самопроизвольного испускания все равны друг другу. В этом смысл соотношения между коэффициентами А и В, выведенного Эйнштейном [см. гл. 42 (вып. 4), соотношение (42.18)].

§ 5. Спектр абсолютно черного тела

Мы хотим теперь использовать наши правила для бозе-частиц, чтобы еще раз получить спектр излучения абсолютно черного тела [см. гл. 42 (вып. 4)]. Мы сделаем это, подсчитав, сколько фотонов содержится в ящике, если излучение нахо­дится в тепловом равновесии с атомами в ящике. Допустим, что каждой световой частоте со соответствует определенное количество N атомов с двумя энергетическими состояниями, отличающимися на энергию D Е =hw (фиг. 2.6).

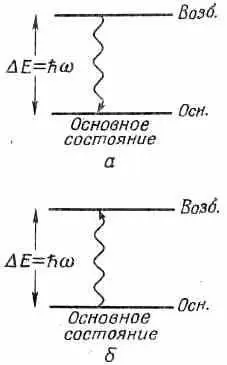
Фиг. 2.6. Излучение и поглощение фотона с частотой w .

Состояние с меньшей энергией мы назовем «основным», с большей — «возбужденным». Пусть N осн и N возб— средние числа атомов в основном и возбужденном состояниях; тогда для теплового равновесия при температуре Т из статистической механики следует

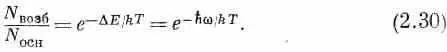
Каждый атом в основном состоянии может поглотить фотон и перейти в возбужденное состояние, и каждый атом в возбу­жденном состоянии может испустить фотон и перейти в основное состояние. При равновесии скорости этих двух процессов должны быть равны. Скорости пропорциональны вероятности событий и количеству имеющихся атомов. Пусть n — среднее число фотонов, находящихся в данном состоянии с частотой w. Тогда скорость поглощения из этого состояния есть N oc н n | а | 2 , а скорость испускания в это состояние есть N возб ( n +1)| а | 2, Приравнивая друг другу эти две скорости, мы получаем

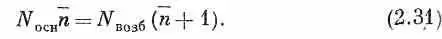
Сопоставляя это с (2.30), имеем

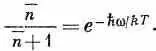
Отсюда найдем

Это и есть среднее число фотонов в любом состоянии с частотой w при тепловом равновесии в полости. Поскольку энергия каждого фотона hw, то энергия фотонов в данном состоянии

есть nh w , или

Кстати говоря, мы уже получали подобное выражение в другой связи [см. гл. 41 (вып. 4), формула (41.15)]. Вспомните, что для гармонического осциллятора (скажем, грузика на пружинке) квантовомеханические уровни энергии находятся друг от друга на равных расстояниях hw, как показано на фиг. 2.7.

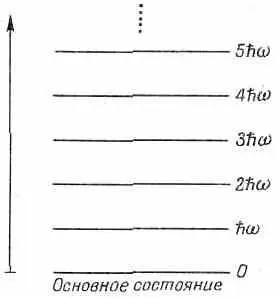
Фиг. 2.7. Уровни энергии гармонического осциллятора.

Обозначив энергию n -го уровня через nh w. мы получили, что средняя энергия такого осциллятора также давалась выражением (2.33). А сейчас это выражение было выведено для фо­тонов путем подсчета их числа и привело к тому же результату. Перед вами — одно из чудес квантовой механики. Если начать с рассмотрения таких состояний или таких условий для бозе-частиц, когда они друг с другом не взаимодействуют (мы ведь предположили, что фотоны не взаимодействуют друг с другом), а за­тем считать, что в эти состояния могут быть помещены нуль, или одна, или две и т. д. до n частиц, то оказывается, что эта система ведет себя во всех квантовомеханических отношениях в точности, как гармонический осциллятор. Таким осциллято­ром считается динамическая система наподобие грузика на пружинке или стоячей волны в резонансной полости. Вот по­чему можно представлять электромагнитное поле фотонными частицами. С одной точки зрения можно анализировать электро­магнитное поле в ящике или полости в терминах множества гармонических осцилляторов, рассматривая каждый тип коле­баний, согласно квантовой механике, как гармонический ос­циллятор. С другой, отличной точки зрения ту же физику можно анализировать в терминах тождественных бозе-частиц. И итоги обоих способов рассуждений всегда точно совпадают. Невоз­можно установить, следует ли на самом деле электромагнитное поле описывать в виде квантуемого гармонического осциллято­ра или же задавать количество фотонов в каждом состоянии. Оба взгляда на вещи оказываются математически тождествен­ными. В будущем мы сможем с равным правом говорить либо о числе фотонов в некотором состоянии в ящике, либо о номере уровня энергии, связанного с некоторым типом колебаний электромагнитного поля. Это два способа говорить об одном и том же. То же относится и к фотонам в пустом пространстве. Они эквивалентны колебаниям полости, стенки которой отошли на бесконечность.