Feynmann - Feynmann 7

Каждый из вас, кто в прошлом работал или бывал в саду или на винограднике, знаком с этим любопытным зрелищем. Посмотрев в одну сторону, вы видите линию деревьев, а если посмотрите в другую,— вам откроется совсем другой ряд и т. д. Так и в кристалле — там есть определенные семейства плоскостей, содержащие много атомов; у таких плоскостей есть важная особенность (для простоты рассмотрим кубический кристалл). Если мы отметим, где эти плоскости пересекаются с тремя осями координат, то окажется, что обратные величины расстояний трех точек пересечения от начала относятся как целые числа. Эти три целых числа и принимаются для обозначения плоскостей. На фиг. 37.7, а, например, показана плоскость, параллельная плоскости yz . Она называется плос­костью (100), так как обратные величины отрезков, отсекае­мых этой плоскостью по осям у и z, равны нулю.

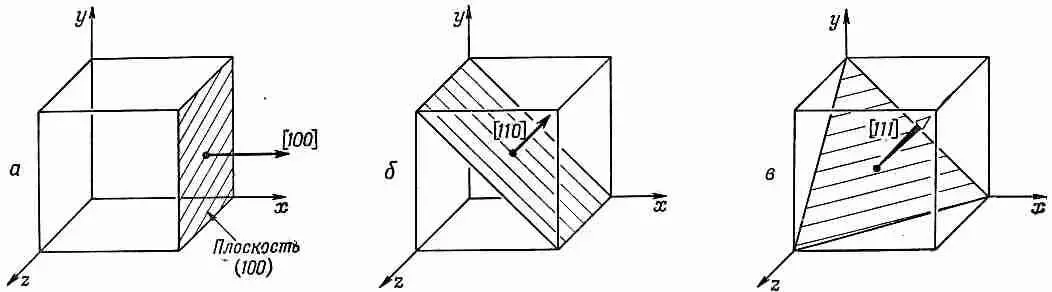
Фиг. 37.7. Способы обозначения кристаллических плоскостей.

Направление, перпендикулярное этой плоскости (в кубическом кристалле), задается тем же самым набором чисел, но записывается в квад­ратных скобках: [100]. Основную идею в случае кубического кристалла понять очень легко, ибо символ [100] обозначает вектор, который имеет единичную компоненту в направлении оси х и нулевые в направлениях осей у и . z . Комбинация [110] обозначает направление под 45° к осям x и y, как показано на фиг. 37.7, б, а [111] — направление диагонали куба (фиг. 37.7,в).

Вернемся теперь к фиг. 37.6. На ней мы видим кривые на­магничивания монокристалла в различных направлениях. Прежде всего заметьте, что для очень слабых полей, столь сла­бых, что в нашем масштабе их трудно изобразить, намагничен­ность чрезвычайно быстро возрастает до весьма больших зна­чений. Если приложить поле в направлении [100], т. е. в одном из направлений легкого намагничивания, то кривая идет вверх до еще большего значения, затем несколько закругляется и наступает насыщение. Происходит это потому, что домены, которые уже там есть, ликвидируются очень легко. Чтобы пе­редвинуть доменные стенки и «проглотить» все «неправильные» домены, требуется совсем слабое поле. Монокристаллы железа обладают огромной проницаемостью (в магнитном смысле), гораздо большей, чем поликристаллическое железо. Совер­шенный кристалл намагничивается очень легко. Почему же его кривая все же закругляется? Почему она не идет прямо до на­сыщения? Точно не известно. Быть может, вам когда-нибудь удастся изучить это явление. Мы понимаем, почему при боль­ших полях она плоская. Когда весь кубик становится единым доменом, то добавочное магнитное поле не может создать боль­шей намагниченности, она уже равна M нас— значит, спины всех электронов направлены вверх.

Что получится, если мы попытаемся повторить то же самое для направления [110], которое лежит в плоскости ху под уг­лом 45° к оси х? Мы включаем небольшое поле, и намагничен­ность за счет роста домена резко увеличивается. Если затем мы продолжаем увеличивать поле, то выясняется, что для достиже­ния насыщения поле должно быть довольно большим, ибо век­тор намагниченности нужно повернуть в сторону от направле­ния легкого намагничивания. Если это объяснение правильно, то при экстраполяции кривой [110] точка пересечения с верти­кальной осью должна будет давать значение намагниченно­сти, составляющее 1/Ц2 от намагниченности насыщения. Ока­зывается, что так оно на самом деле и происходит. Это отношение очень-очень близко к 1/Ц2. Аналогично для направ­ления [111], которое идет по диагонали куба, мы находим, как и ожидали, что при экстраполяции кривая пересекает вер­тикальную ось на расстоянии, составляющем 1/Ц2 от значе­ния, соответствующего насыщению.

На фиг. 37.8 показано соответствующее поведение двух других ферромагнетиков: никеля и кобальта.

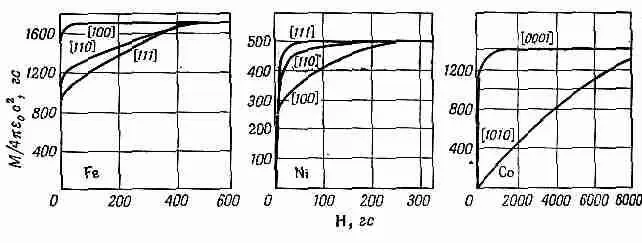
Фиг. 37.8. Кривые намагничивания для монокристаллов железа, никеля и кобальта.

Никель отличает­ся от железа. Оказывается, что направлением легкого намаг­ничивания у него будет направление [111]. Кобальт имеет гек­сагональную кристаллическую структуру; для этого случая система обозначений была изменена. Здесь в основании шестиугольника располагают три оси и еще одну ось, перпендикуляр­ную к ним, так что здесь используется четыре числа. Направ­ление [0001] — это направление гексагональной оси, а [1010]— направление, перпендикулярное к этой оси. Вы видите, что кристаллы различных металлов устроены по-разному.