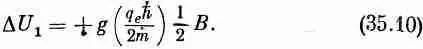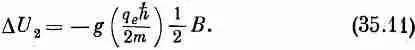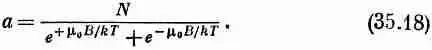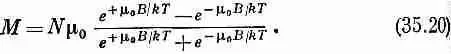Feynmann - Feynmann 7

[См. выражение (11.20), вып. 5.] Эта приближенная формула верна, только когда отношение m B / kT много меньше единицы.

Мы нашли, что намагниченность, т. е. магнитный момент единицы объема, пропорциональна магнитному полю. Это яв­ление и называется парамагнетизмом. Вы увидите, что эффект сильнее проявляется при низких температурах и слабее при высоких. При помещении вещества в магнитное поле возникаю­щий в нем магнитный момент в случае слабых полей пропор­ционален величине поля. Отношение М к В (для слабых полей) называется магнитной восприимчивостью.

Рассмотрим теперь парамагнетизм с точки зрения квантовой механики. Обратимся сначала к атомам со спином 1 / 2 . Если в отсутствие магнитного поля атомы обладают вполне определенной энергией, то в магнитном поле энергия изменится; возможны два значения энергии для разных значений J z. Для J z=+h/2

магнитное поле изменяет энергию на величину

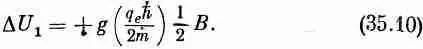
(Для атомов сдвиг энергии DU положителен, ибо заряд элек­трона отрицателен.) Для J г=- h/2 энергия изменяется на величину

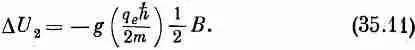
Для сокращения записи обозначим

тогда

D U = ± m 0 В. (35.13)

Совершенно ясен и смысл m 0; — m 0 равно z-компоненте маг­нитного момента для спина, направленного вверх, а + m 0равно z-компоненте магнитного момента в случае спина, на­правленного вниз.

Статистическая механика говорит нам, что вероятность нахождения атома в каком-то состоянии пропорциональна

g - (энергия состояния)/ kT .

В отсутствие магнитного поля энергия обоих состояний одна и та же, поэтому в случае равновесия в магнитном поле ве­роятности пропорциональны

е - D U / kT , (35.14)

Число же атомов в единице объема со спином, направленным вверх, равно

а со спином, направленным вниз,

Постоянная а должна определяться из условия

N вверх+N вниз=N (35.17)

т.е. равна полному числу атомов в единице объема. Таким образом, мы получаем

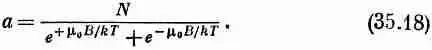
Однако нас интересует средний магнитный момент в на­правлении оси z . Каждый атом со спином, направленным вверх, дает в этот момент вклад, равный -m 0, а со спином, направленным вниз, + m 0, так что средний момент будет

Тогда М — магнитный момент единицы объема — будет равен N ср. Воспользовавшись выражениями (35.15)—(35.17), по­лучим

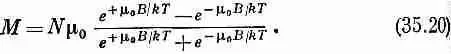
Это и есть квантовомеханическая формула для М в случае атомов со спином j= 1/ 2. К счастью, ее можно записать более коротко через гиперболический тангенс:

График зависимости М он В приведен на фиг. 35.7.

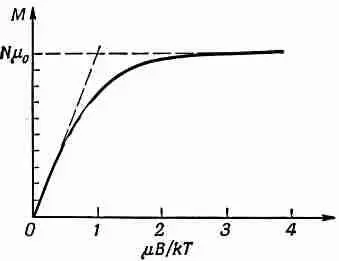
Фиг. 35.7. Изменение намаг­ниченности парамагнетика при изменении напряженности магнитного поля В .

Когда поле В становится очень большим, гиперболический тангенс приближается к единице, а М — к своему предельному зна­чению Nm 0. Таким образом, при сильных полях происходит насыщение. Нетрудно понять, почему так получается — ведь при достаточно больших полях все магнитные моменты выстраи­ваются в одном и том же направлении. Другими словами, при насыщении все атомы находятся в состоянии со спинами, направленными вниз, и каждый из них дает вклад в магнитный момент, равный m 0.