Feynmann - Feynmann 7

В гл. 11 (вып. 5) мы описывали сегнетоэлектрические ма­териалы, все электрические диполи которых выстраиваются в результате взаимного действия атомов друг на друга своими электрическими полями. Можно представить себе магнитный аналог сегнетоэлектричества, в котором все атомные моменты, действуя друг на друга, выстраивают сами себя. Если бы вы попытались вычислить, как это должно происходить, то обнару­жили бы, что из-за того, что магнитные силы гораздо слабее электрических, тепловое движение должно расстраивать упо­рядочивание даже при столь низких температурах, как 10° К. Так что при комнатных температурах любое постоянное вы­страивание магнитных моментов казалось бы невозможно.

Но, с другой стороны, именно это явление происходит в же­лезе: там магнитные моменты все-таки выстраиваются. Между магнитными моментами различных атомов железа действуют эффективные силы, которые во много-много раз больше прямого магнитного взаимодействия. Это косвенный эффект, кото­рый можно объяснить только с помощью квантовой механики. Он примерно в десять тысяч раз сильнее прямого магнитного взаимодействия, и именно он выстраивает магнитные моменты в ферромагнитных материалах. Об этом особом взаимодействии мы будем говорить в дальнейшем.

Я попытался дать вам качественные объяснения диамагне­тизма и парамагнетизма, однако хочу тут же внести поправку и сказать, что с точки зрения классической механики честным путем понять магнитные эффекты невозможно. Подобные маг­нитные эффекты — явления целиком квантовомеханические. Тем не менее привести некоторые «правдоподобные» классические рассуждения и дать вам представление о том, как здесь все происходит, все-таки небесполезно.

Попробуем встать на этот путь. Можно приводить разные фи­зические аргументы и строить догадки о том, что происходит с веществом, однако все эти аргументы будут в той или иной степени «незаконными», так как в любом из магнитных явлений весьма существенную роль играет квантовая механика. С другой стороны, бывают такие системы, подобные плазме или скопле­нию множества свободных электронов, где электроны все же живут по законам классической механики. При таких обстоя­тельствах некоторые из теорем классического магнетизма будут очень полезны. Кроме того, классические рассуждения полезны еще и по историческим причинам: ведь пока люди еще не могли понять глубокий смысл и поведение магнитных материалов, они пользовались классическими аргументами. Так что клас­сическая механика все же способна дать нам полезные сведения. И только если стремиться быть совсем честным, то надо отложить изучение магнетизма до тех пор, пока вы не пройдете квантовую механику.

А мне все-таки не хочется ждать так долго ради того, чтобы понять такую простую вещь, как диамагнетизм. Для целого ряда полуобъяснений происходящего можно ограничиться клас­сической механикой, сознавая, однако, что наши доводы на самом деле нуждаются в квантовомеханическом подкреплении.

§ 2. Магнитные моменты и момент количества движения

Первая теорема, которую мы хотим доказать в классической механике, гласит: если электрон движется по круговой орбите (например, крутится вокруг ядра под действием центральных сил), то менаду магнитным моментом и моментом количества движения существует определенное соотношение. Обозначим через Jмомент количества движения, а через m — магнитный момент электрона на орбите. Величина момента количества движения равна произведению массы электрона на скорость и на радиус (фиг. 34.2). Он направлен перпендикулярно плоскости орбиты:

J =mvr. (34.1)

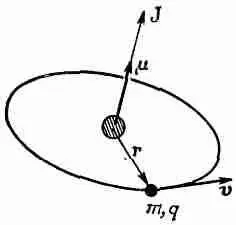
Фиг. 34.2. Для любой круговой орбиты магнитный момент m равен произведению q !2 m на момент количества движения J .

(Хотя эта формула и нерелятивистская, но для атома она должна быть достаточно хороша, ибо у захваченного на орбиту элект­рона отношение v / c в общем случае равно по порядку величины е 2/hc=1/137, или около 1%.)

Магнитный момент той же самой орбиты равен произведению тока на площадь (см. гл. 14, § 5, вып. 5). Ток равен положи­тельному заряду, проходящему в единицу времени через любую точку на орбите, т. е. произведению заряда q на частоту вра­щения. А частота равна скорости, поделенной на периметр орбиты, так что