Feynmann - Feynmann 7

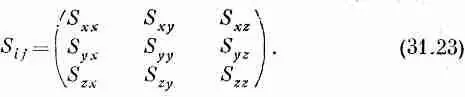
Фиг. 31.5. Материал, находящийся слева от плоскости s на площади D y / D z , действует на материал, нахо­дящийся справа, с силой D F 1 .

Материал, находящийся слева от площадки, действует на материал с правой стороны с силой D F 1(фиг. 31.5, б). Есть, конечно, и обратная реакция, т.е. на материал слева от поверхности действует сила —D F 1. Если площадка достаточно мала, то мы ожидаем, что сила D F 1про­порциональна площади Dy/Dz.

Вы уже знакомы с одним видом напряжений — статическим давлением жидкости. Там сила была равна давлению, умно­женному на площадь, и направлена под прямым углом к элементу поверхности. Для твердого тела, а также движущей­ся вязкой жидкости сила не обязательно перпендикулярна по­верхности: помимо давления (положительного или отрицатель­ного), появляется еще и сдвигающая сила. (Под «сдвигающей» силой мы подразумеваем тангенциальные компоненты сил, действующих на поверхности.) Для этого нужно учитывать все три компоненты силы. Заметьте еще, что если раз­рез мы сделаем по плоскости с какой-то другой ориента­цией, то действующие на ней силы тоже будут другими. Полное описание внутренних напряжений требует применения тензоров.

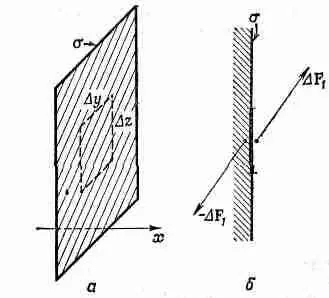
Определим тензор нап­ряжений следующим образом. Вообразите сначала разрез, перпендикулярный оси х, и разложите силу DF 1, действующую на разрезе, на ее компо­ненты: DF x 1, DF y 1, DF z 1(фиг. 31.6).

Фиг. 31.6. Сила DF 1, дейст­вующая на элементе площади DyDz, перпендикулярной оси х, разлагается на три компонен­ты: DF x 1, DF у 1 и D F z 1 .

Отношение этих сил к площади Dy/Dz мы назовем S xx , S yx и S zx . Например,

S yx = DF у 1 / DyDz

Первый индекс у относится к направлению компоненты силы, а второй х — к направлению нормали к плоскости. Если угод­но, площадь DyDz можно записать как D а х , имея в виду элемент площади, перпендикулярный оси х, т. е.

S yx = DF у 1 / D а х

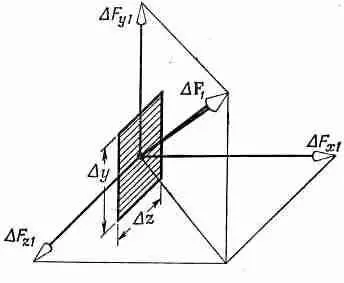
А теперь представьте себе разрез, перпендикулярный оси у. Пусть на маленькую площадку DxDz действует сила D F 2.

Разлагая снова эту силу на три компоненты, как показано на фиг. 31.7, мы опре­деляем три компоненты на­пряжения S xy , S yy , S zy как силы, действующие на единичную площадь в этих трех направлениях.

Фиг. 31.7. Сила, действующая на элемент площади, перпенди­кулярной оси у, разлагается на три взаимно перпендикулярные компоненты.

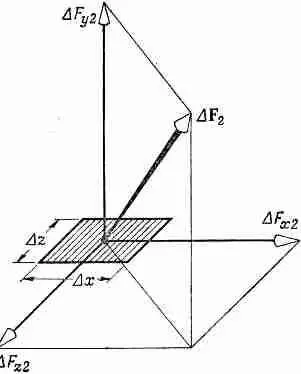
Наконец, проведем воображаемый раз­рез, перпендикулярный оси z, и определим три компоненты S xz , S yz и S zz . Таким образом, получается девять чисел:

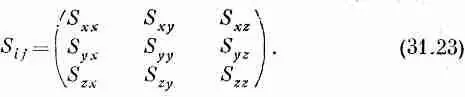
Я хочу теперь показать, что этих девяти величин достаточ­но, чтобы полностью описать внутреннее напряженное состоя­ние, и что S ij - — действительно тензор. Предположим, что мы хо­тим знать силу, действующую на поверхность, наклоненную под некоторым произвольным углом. Можно ли найти ее, ис­ходя из S ij ? Можно, и это делается следующим образом. Вооб­разите маленькую призму, одна грань N которой наклонна, а другие — параллельны осям координат. Если окажется, что грань N параллельна оси z , то получается картина, изобра­женная на фиг. 31.8.

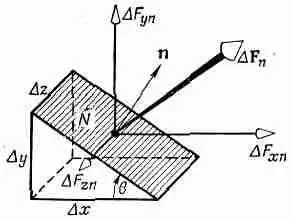
Фиг. 31.8. Разложение на компо­ненты силы F n, действующей на грани N (с единичной нормалью n ) .

(Это, конечно, частный случай, но он до­статочно хорошо иллюстрирует общий метод.) Дальше, напря­жения, действующие на эту призмочку, должны быть такими, чтобы она находилась в равновесии (по крайней мере в пределе бесконечно малого размера), так что действующая на нее пол­ная сила должна быть равна нулю. Силы, действующие на гра­ни, параллельные осям координат, известны нам непосред­ственно из тензора S ij . А их векторная сумма должна равняться силе, действующей на грань N, так что эту силу можно выра­зить через S ij .