Feynmann - Feynmann 6

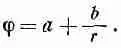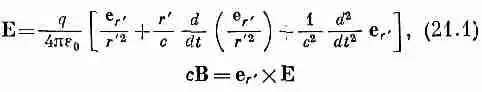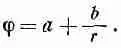
где b — другая постоянная интегрирования. Итак, мы обна­ружили, что решение для электростатического потенциала в пустом пространстве имеет вид

Что-то здесь явно не так. Мы же знаем решение для электро­статического потенциала в области, где нет электрических за­рядов: потенциал всюду постоянен. Это соответствует первому слагаемому в решении. Но имеется еще и второй член, подска­зывающий нам, что в потенциал дает вклад нечто, меняющееся как 1/r. Мы знаем, однако, что подобный потенциал соответ­ствует точечному заряду в начале координат. Стало быть, хоть мы и думали, что нашли решение для потенциала в пустом про­странстве, наше решение фактически дает нам также поле то­чечного источника в начале координат. Вы замечаете сходство между тем, что сейчас произошло, и тем, что произошло тогда, когда мы искали сферически симметричное решение волнового уравнения? Если бы в начале координат действительно не было ни зарядов, ни токов, то не возникли бы и сферически расходя­щиеся волны. Сферические волны должны вызываться источни­ками в начале координат. В следующей главе мы исследуем связь между излучаемыми электромагнитными волнами и вызы­вающими их токами и напряжениями.

Глав а 21

РЕШЕНИЯ УРАВНЕНИЙ МАКСВЕЛЛА С ТОКАМИ И ЗАРЯДАМИ

§ 1. Свет и электро­магнитные волны

§ 2. Сферические вол­ны от точечного источника

§ 3. Общее решение уравнений Максвелла

§ 4. Поля колеблющегося диполя

§ 5. Потенциалы дви­жущегося заряда; общее реше­ние Льенара и

Вихерта

§ 6. Потенциалы заряда, движущегося с постоянной скоростью;

формула Лоренца

Повторить: гл. 28 (вып. 3) «Элект­ромагнитное излучение»; гл. 31 (вып. 3)

«Как возникает показатель преломления»; гл. 34 (вып. 3)

«Релятивистские явления в излучении»

§ 1. Свет и электромагнитные волны

В предыдущей главе мы видели, что среди решений уравнений Максвелла есть электро­магнитные волны. Свету, радио, рентгеновским лучам и т. д. отвечают электромагнитные волны отличающиеся только длиной волны. Мы уже подробно изучали различные явления, связан­ные со светом. В этой главе мы хотим связать оба вопроса и показать, что уравнения Мак­свелла действительно могли служить основой для изучения свойств света.

Наше изучение света мы начали с того, что выписали уравнение для электрического поля, создаваемого зарядом, который мог как-то произвольно двигаться. Уравнение имело вид

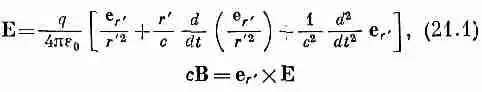
[см. гл. 28 (вып. 3), выражение (28.3)].

Если заряд движется произвольным обра­зом, то электрическое поле, которое существует в некоторой точке, в настоящий момент за­висит только от положения и движения заряда в более ранний момент времени, отстающий на интервал, необходимый для того, чтобы свет, двигаясь со скоростью с, прошел расстояние r ' от заряда до точки поля. Иными словами, если вам нужно знать электрическое поле в точке (1) в момент t , вы должны подсчитать положение (2') заряда и его движение в момент ( t - r '1с} [где r ' — расстояние до точки (1)] из положения заряда (2') в момент ( t — r / с).

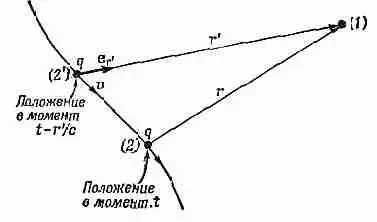
Фиг. 21.1. Поля в точке (1) в момент t зависят от того положения (2'), которое заряд q занимал в момент ( t — r ' / с).

Штрихи здесь напоминают вам, что r ' — это так называемое «запаздывающее расстояние» от точки (2') к точке (1), а вовсе не теперешнее расстояние между точкой (2) — положением за­ряда в момент t — и точкой поля (1) (фиг. 21.1). Заметьте, что сейчас по-иному определяется направление единичного век­тора е r . В гл. 28 и 34 (вып. 3) мы уславливались, что r (и, стало быть, е r) будет показывать на источник. Теперь же мы следуем определению, используемому в формулировке закона Кулона, по которому r направлено от заряда [в точке (2)] к точке (1) поля. Единственное отличие в том, что новое r (и е r) противо­положно старому.