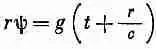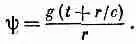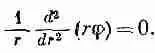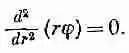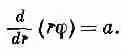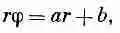Feynmann - Feynmann 6

Фиг. 20.6. Сферическая волна ш=f(t-r /с)/ r .

а — зависимость ш от r при t = t l и ma же волна в более поздний момент времени t 2; б — зависимость ш от t при r =r 1 и та же самая волна на расстоянии r 2.

Этот факт легко понять из про­стых физических соображений.

Мы знаем, что плотность энергии в волне зависит от квадрата амплитуды волны. По мере того как волна разбегается, ее энергия расплывается на все большую и большую площадь, пропорциональную квадрату радиуса волны. Если полная энер­гия сохраняется, плотность энергии должна убывать как 1/r 2, а амплитуда — как 1/r. Поэтому формула (20.35) для сфери­ческой волны вполне «разумна».

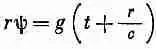
Мы игнорировали другое возможное решение одномерного волнового уравнения

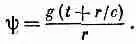
или

Это тоже сферическая волна, но бегущая внутрь, от больших r к началу координат.

Тем самым мы делаем некоторое специальное предположе­ние. Мы утверждаем (без какого-либо доказательства), что волны, создаваемые источником, всегда бегут только от него. Поскольку мы знаем, что волны вызываются движением заря­дов, мы настраиваемся на то, что волны бегут от зарядов. Было бы довольно странно представлять, что прежде чем заряды были приведены в движение, сферическая волна уже вышла из бесконечности и прибыла к зарядам как раз в тот момент, когда они начали шевелиться. Такое решение возможно, но опыт по­казывает, что, когда заряды ускоряются, волны распростра­няются от зарядов, а не к ним. Хоть уравнения Максвелла предоставляют обеим волнам равные возможности, мы привле­каем добавочный факт, основанный на опыте, что «физическим смыслом» обладает только расходящаяся волна.

Нужно, однако, заметить, что из этого добавочного пред­положения вытекает интересное следствие: мы теряем при этом симметрию относительно времени, которая есть у уравнений Максвелла. Как исходные уравнения для Е и В, так и вытекающие из них волновые уравнения при изменении знака t не ме­няются. Эти уравнения утверждают, что любому решению, ко­торое отвечает волне, бегущей в одну сторону, отвечает столь же правильное решение для волны, бегущей в обратную сторону. И утверждая, что мы намерены брать в расчет только расходя­щиеся сферические волны, мы делаем тем самым важное допол­нительное предположение. (Очень тщательно изучалась такая электродинамика, в которой обходятся без этого дополнитель­ного предположения. Как это ни удивительно, но во многих обстоятельствах она не приводит к физически абсурдным ре­зультатам. Однако обсуждение этих идей теперь увлекло бы нас чересчур в сторону. Мы поговорим об этом подробнее в гл. 28.)

Нужно упомянуть еще об одном важном факте. В нашем решении для расходящейся волны (20.35) функция ш в начале ко­ординат бесконечна. Это как-то необычно. Мы бы предпочли иметь такие волновые решения, которые гладки повсюду. Наше решение физически относится к такой ситуации, когда в начале координат располагается источник. Значит, мы нечаянно сде­лали одну ошибку: наша формула (20.35) не является решением свободного волнового уравнения (20.33) повсюду; уравнение (20.33) с нулем в правой части решено повсюду, кроме начала координат. Ошибка вкралась оттого, что некоторые действия при выводе уравнения при r=0 «незаконны».

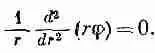
Покажем, что ту же самую ошибку легко сделать и в элект­ростатике. Допустим, что нам нужно решить уравнение элек­тростатического потенциала в пустом пространстве С 2j=0. Лапласиан равен нулю, потому что мы предположили, что ни­каких зарядов нигде нет. Но как обстоит дело со сферически симметричным решением уравнения, т. е. с функцией j, зависящей только от r? Используя для лапласиана формулу (20.32), получаем

Умножив это выражение на r, приходим к уже интегрировав­шемуся уравнению

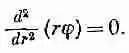
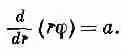
Проинтегрировав один раз по r , мы увидим, что первая про­изводная rj равна постоянной, которую мы обозначим через а;

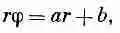
Еще раз проинтегрировав, мы получим для rj формулу