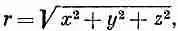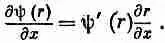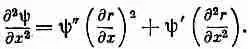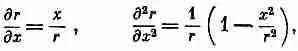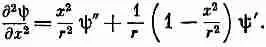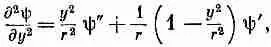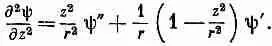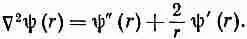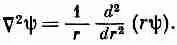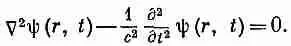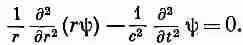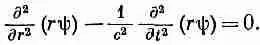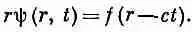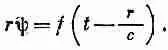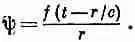Feynmann - Feynmann 6

Прежде чем начать описание сферических волн, немного зай­мемся математикой. Пусть имеется функция, зависящая только от радиального расстояния r точки от начала координат, иными словами, сферически симметричная функция. Обозначим ее ш(r), где под r подразумевается

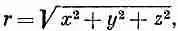
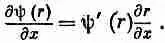
т. е. расстояние от начала координат. Чтобы узнать, какие функ­ции ш (r) удовлетворяют волновому уравнению, нам понадо­бится выражение для лапласиана ш. Значит, нам нужно найти сумму вторых производных ш по х, по у и по z. Через ш'(r) мы обозначим первую производную i|) по r, а через ш"(r) — вторую. Сначала найдем производные по х. Первая производная равна

Вторая производная по х равна

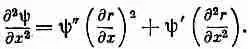
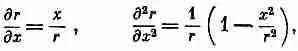
Частные производные r по x можно получить из

так что вторая производная ш no x принимает вид

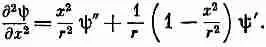
(20.28)

Точно так же и

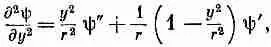
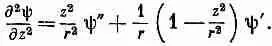
(20.29)

(20.30)

Лапласиан равен сумме этих трех производных. Вспоминая,

что x 2+y 2+z 2=r 2, получаем

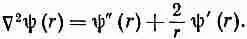
(20.31)

Часто бывает удобнее записывать уравнение в следующей

форме:

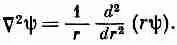
(20.32)

Проделав дифференцирование, указанное в (20.32), вы убеди­тесь, что правая часть здесь та же, что и в (20.31).

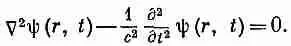
Если мы хотим рассматривать сферически симметричные поля, которые могут распространяться как сферические волны, то ве­личины, описывающие поля, должны быть функцией как r , так и t . Предположим, что нам нужно знать, какие функции ш(r, t ) являются решениями трехмерного волнового уравне­ния

(20.33)

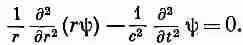
Поскольку ш(г, t ) зависит от пространственных координат только через г, то в качестве лапласиана можно использовать выражение (20.32). Но для точности, поскольку ш зависит также и от t , нужно дифференцирование по r записывать в виде частной производной. Волновое уравнение обращается в

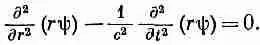
Его и предстоит нам решать. Оно выглядит сложнее, чем в случае плоских волн. Но заметьте, что если умножить это урав­нение на r, то получится

(20.34)

Это уравнение говорит нам, что функция rш удовлетворяет одномерному волновому уравнению по переменной r. Исполь­зуя часто подчеркивавшийся нами общий принцип, что у одних и тех же уравнений и решения одни и те же, мы приходим к выводу, что если rш окажется функцией одного только (r- ct ), то оно явится решением уравнения (20.34). Итак, мы обнаружи­ваем, что сферические волны обязаны иметь вид

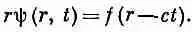
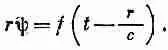
Или, как мы видели раньше, можно в равной степени считать rш имеющим форму

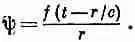
Деля на r, находим, что характеризующая поле величина ш (чем бы она ни была) имеет вид

(20.35)

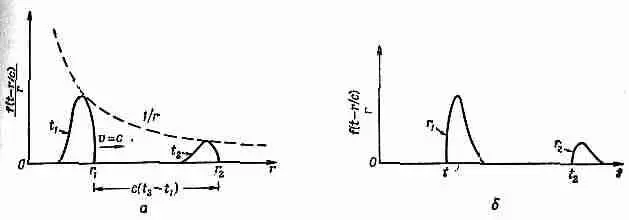
Такая функция представляет сферическую волну общего вида, распространяющуюся от начала координат со скоростью с. Если на минуту забыть об r в знаменателе, то амплитуда волны как функция расстояния от начала координат в каждый данный момент обладает определенной формой, которая рас­пространяется со скоростью с. Однако r в знаменателе говорит нам, что по мере того, как волна распространяется, ее амплиту­да убывает пропорционально 1/r. Иными словами, в отличие от плоской волны, амплитуда которой остается при движении все время одной и той же, амплитуда сферической волны бес­прерывно спадает (фиг. 20.6).