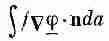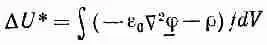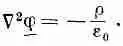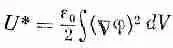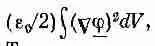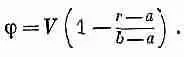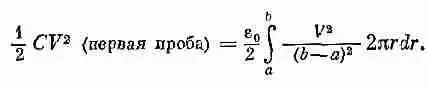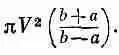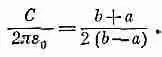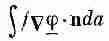
тоже равен нулю. Остающееся объемное интегрирование нужно проделывать только в промежутках между проводниками.
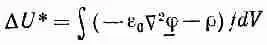
И мы, конечно, снова получаем уравнение Пуассона
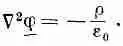
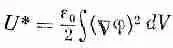
Мы, стало быть, показали, что наш первоначальный интеграл U * достигает минимума и тогда, когда он вычисляется в пространстве между проводниками, каждый из которых находится при фиксированном потенциале [это значит, что каждая пробная функция j (х, у, z ) должна равняться заданному потенциалу проводника, когда (х, у, z ) — точки поверхности проводника]. Существует интересный частный случай, когда заряды расположены только на проводниках. Тогда
и наш принцип минимума говорит нам, что в случае, когда у каждого проводника есть свой заранее заданный потенциал, потенциалы в промежутках между ними пригоняются так, что интеграл U * оказывается как можно меньше. А что это за интеграл? Член Сj — это электрическое поле. Значит, интеграл — это электростатическая энергия. Правильное поле и есть то единственное, которое из всех полей, получаемых как градиент потенциала, отличается наименьшей полной энергией.
Я хотел бы воспользоваться этим результатом, чтобы решить какую-нибудь частную задачу и показать вам, что все эти вещи имеют реальное практическое значение. Предположим, что я взял два проводника в форме цилиндрического конденсатора.

У внутреннего проводника потенциал равен, скажем, V , а у внешнего— нулю. Пусть радиус внутреннего проводника будет равен а, а внешнего — b . Теперь мы можем предположить, что распределение потенциалов между ними — любое.
Но если мы возьмем правильное значение j и вычислим
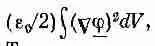
, то должна получиться энергия системы 1/ 2CV 2.
Так что с помощью нашего принципа можно подсчитать и емкость С. Если же мы возьмем неправильное распределение потенциала и попытаемся этим методом прикинуть емкость конденсатора, то придем к чересчур большому значению емкости при фиксированном V . Любой предполагаемый потенциал j, не точно совпадающий с истинным его значением, приведет и к неверной величине С, большей, чем нужно. Но если неверно выбранный потенциал j является еще грубым приближением, то емкость С получится уже с хорошей точностью, потому что погрешность в С — величина второго порядка по сравнению с погрешностью в j.
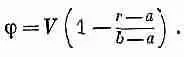
Предположим, что мне неизвестна емкость цилиндрического конденсатора. Тогда, чтобы узнать ее, я могу воспользоваться этим принципом. Я просто буду испытывать в качестве потенциала разные функции j до тех пор, пока не добьюсь наинизшего значения С. Допустим, к примеру, что я выбрал потенциал, отвечающий постоянному полю. (Вы, конечно, знаете, что на самом деле поле здесь не постоянно; оно меняется как 1/r.) Если поле постоянно, то это означает, что потенциал линейно зависит от расстояния. Чтобы напряжение на проводниках было каким нужно, функция j должна иметь вид
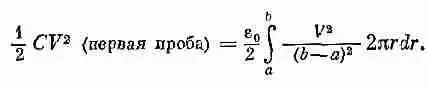
Эта функция равна V при r =а, нулю при r=b, а между ними имеется постоянный наклон, равный — V /( b - а). Значит, чтобы определить интеграл U*, надо только помножить квадрат этого градиента на e 0/2 и проинтегрировать по всему объему. Проведем этот расчет для цилиндра единичной длины. Элемент объема при радиусе r равен 2 p rdr . Проводя интегрирование, я нахожу, что моя первая проба дает такую емкость:
Интеграл здесь просто равен
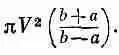
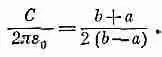
Читать дальше