Feynmann - Feynmann 6a

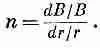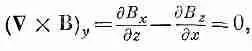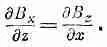
Другая трудность, связанная с однородным полем, состоит в том, что частицы не остаются в одной плоскости. Если они начинают движение под небольшим углом или небольшой угол создается неточностью поля, то частицы идут по спираль­ному пути, который в конце концов приведет их либо на полюс магнита, либо на по­толок или пол вакуумной камеры.

Фиг. 29.10. Движение частицы в слабо неоднородном поле.

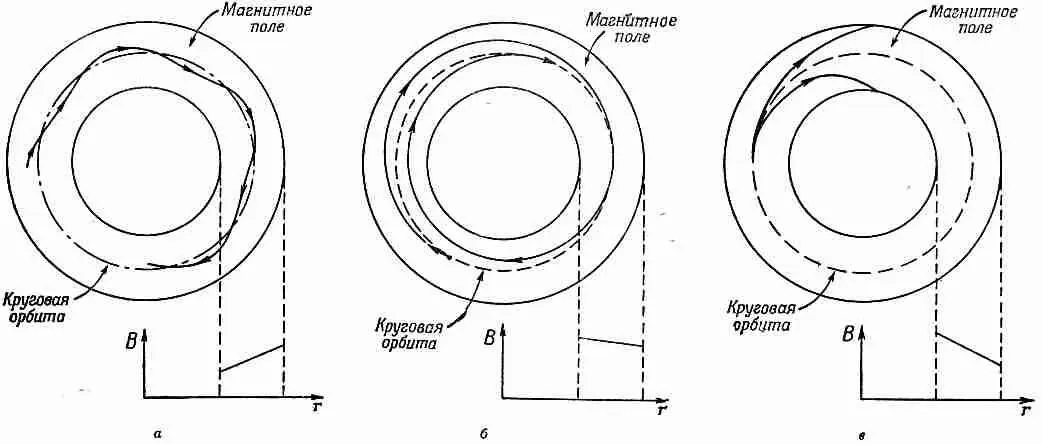
Ф и г . 29.11. Радиальное движение частицы в магнитном поле.

а — с большим положительным «наклоном»; б — с малым отрицательным «наклоном»; в — с большим отрицательным «наклоном».

Чтобы избежать такого вертикального дрейфа, нужны какие-то устройства; магнитное поле должно обеспечивать как радиальную, так и «вертикальную» фокусировки.

Сразу же можно догадаться, что радиальную фокусировку обеспечивает созданное магнитное поле, которое увеличивается с ростом расстояния от центра проектируемого пути. Тогда, если частица выйдет на больший радиус, она окажется в более сильном поле, которое вернет ее назад на нужную орбиту. Если она перейдет на меньший радиус, то «загибание» будет меньше и она снова вернется назад на желаемый радиус. Если частица внезапно начала двигаться под углом к идеальной орбите, она начнет осциллировать относительно нее (фиг. 29.И, а) и радиаль­ная фокусировка будет удерживать частицу вблизи кругового пути.

Фактически радиальная фокусировка происходит даже при противоположном «наклоне». Это может происходить в тех слу­чаях, когда радиус кривизны траектории увеличивается не быстрее, чем расстояние частицы от центра поля. Орбиты частиц будут подобны изображенным на фиг. 29.11,6. Но если градиент поля слишком велик, то частицы не вернутся на желаемый ра­диус, а будут по спирали выходить из поля либо внутрь, либо наружу (фиг. 29.11, в ).

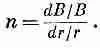
«Наклон» поля мы обычно характеризуем «относительным градиентом», или индексом поля n

(29.2)

Направляющее поле создает радиальную фокусировку, если относительный градиент будет больше -1.

Радиальный градиент поля приведет также к вертикальным силам, действующим на частицу. Предположим, мы имеем поле, которое вблизи центра орбиты сильнее, а снаружи слабее. Вертикальное поперечное сечение магнита под прямым углом к орбите может иметь такой вид, как показано на фиг. 29.12. (Причем протоны летят на нас из страницы.) Если нам нужно, чтобы поле было сильнее слева и слабее справа, то магнитные силовые линии должны быть искривлены подобно изображен­ным на рисунке. То, что это должно быть так, можно уви­деть из закона равенства нулю циркуляции В в пустом прос­

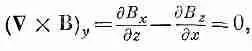
транстве. Если выбрать систему координат, показанную на рисунке, то

или

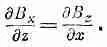
(29.3)

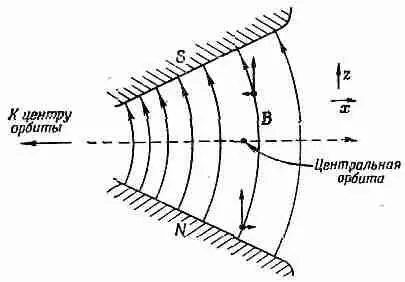
Фиг. 29.12. Вертикаль­но фокусирующее поле.

Вид в поперечном сечении, перпендикулярном к орбите.

Поскольку мы предполагаем, что дВ z /дх отрицательно, то рав­ным ему и отрицательным должно быть и дВ х /д z . Если «номиналь­ной» плоскостью орбиты является плоскость симметрии, где В х =0, то радиальная компонента В х будет отрицательной над плоскостью и положительной под ней. При этом линии должны быть искривлены так, как это изображено на рисунке.

Такое поле должно обладать вертикально фокусирующими свойствами. Представьте себе протон, летящий более или менее параллельно центральной орбите, но выше нее. Горизонтальная компонента В будет действовать на протон с силой, направлен­ной вниз. Если же протон находится ниже центральной орбиты, то сила изменит свое направление. Таким образом, возникает эффективная «восстанавливающая сила», направленная к центру орбиты. Из наших рассуждений получается, что при условии уменьшения вертикального поля с увеличением радиуса должна происходить вертикальная фокусировка. Однако если градиент поля положительный, то происходит «вертикальная дефоку­сировка». Таким образом, для вертикальной фокусировки индекс поля n должен быть меньше нуля. Выше мы нашли, что для ра­диальной фокусировки значение n должно быть больше -1. Комбинация этих двух условий требует для удержания частиц на стабильных орбитах, чтобы