Feynmann - Feynmann 5b

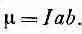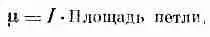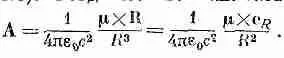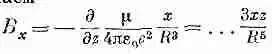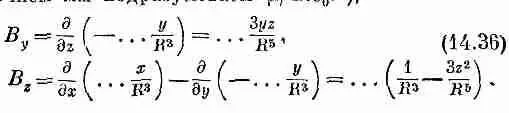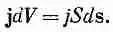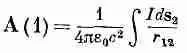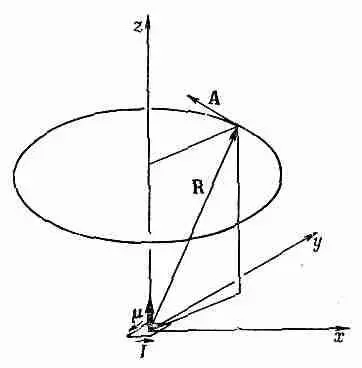
Фиг. 14.8. Векторный потен­циал маленькой петли с током, расположенной в начале коорди­нат (в плоскости ху). Поле магнитного диполя .

Снова А у пропорциональ­но х, а А х пропорцио­нально —y, так что век­торный потенциал (на больших расстояниях) идет по кругу вокруг оси z, циркулируя таким же образом, как ток I в петле (фиг. 14.8).

Величина А пропорциональна I ab , т. е. току, умноженному на площадь петли. Это произведение называется магнитным дипольным моментом (или часто просто «магнитным момен­том») петли. Мы обозначим его через m:

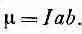
(14.32)

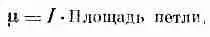
Векторный потенциал маленькой плоской петельки любой формы (круг, треугольник и т. п.) также дается уравнениями (14.30) и (14.31), если заменить I ab на

(14.33)

Мы предоставляем вам право это доказать.

Нашему уравнению можно придать векторную форму, если определить вектор m как нормаль к плоскости петли с поло­жительным направлением, определяемым по правилу правой руки (см. фиг. 14.8). Тогда можно написать

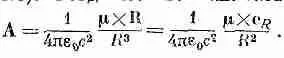
(14.34)

Нам еще нужно найти В. Пользуясь (14.33) и (14.34), а также (14.4). получаем

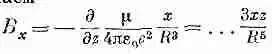
(14.35)

(под многоточием мы подразумеваем m/4pe 0с 2),

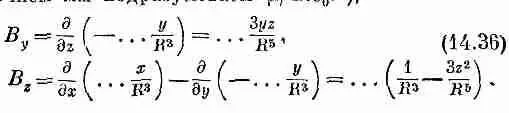
Компоненты поля В ведут себя точно так же, как компоненты поля Е для диполя, ориентированного вдоль оси z [см. уравне­ния (6.14) и (6.15), а также фиг. 6.5, стр. 115]. Вот почему мы называем петлю магнитным диполем. Слово «диполь» в при­менении к магнитному полю немного запутывает, потому что нет отдельных магнитных «полюсов», соответствующих элек­трическим зарядам. Магнитное «дипольное поле» создается не двумя «зарядами», а элементарной петлей с током.

В общем-то довольно любопытно, что, начав с совсем раз­ных законов, С·Е=r/e 0и СXВ=j/e 0с 2, можно прийти к полю одного и того же вида. Почему так получается? Потому что дипольные поля возникают, только когда мы находимся далеко от всех токов и зарядов. Тогда в большей части пространства уравнения для Е и В одинаковы: у обоих дивергенция и ротор равны нулю. Следовательно, они дают одни и те же решения. Однако источники, конфигурацию которых мы описываем с помощью дипольных моментов, физически совершенно различ­ны. В одном случае это циркулирующий ток, а в другом — пара зарядов, один над, а другой под плоскостью петли для соответствующего поля.

§ 6. Векторный потенциал цепи

Нас часто интересует магнитное поле, создаваемое цепью проводов, в которой диаметр провода очень мал по сравнению с размерами всей системы. В таких случаях мы можем упро­стить уравнения для магнитного поля.

Для тонкого провода элемент объема можно записать в виде

dV = Sds ,

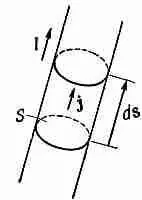
где S — площадь поперечного сечения провода, a ds — эле­мент расстояния вдоль проволоки. В самом деле, поскольку вектор ds имеет то же направление, что и j (фиг. 14.9), и мы можем предположить, что j постоянно по любому данному сечению, то можно записать векторное уравнение

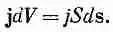
(14.37)

Фиг. 14.9. Для тонкой проволоки jdV то же самое, что и Ids .

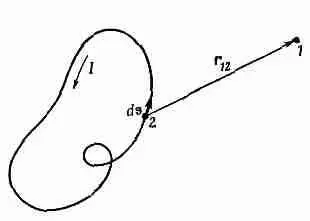
Фиг. 14.10. Магнитное поле провода может быть получено интегрированием по всей цепи.

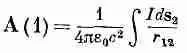
Ho jS — как раз то, что мы называем током I во всем проводе, так что наш интеграл для векторного потенциала (14.19) ста­новится равным

(14.38)

(фиг. 14.10). (Мы предполагаем, что / одно и то же вдоль всего контура. Если есть несколько ответвлений с разными токами, то следует, конечно, брать соответствующий ток в каждой ветви.)