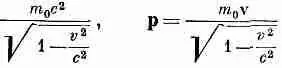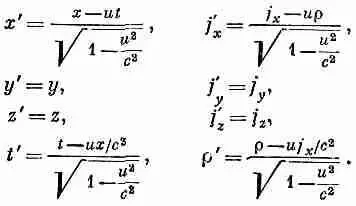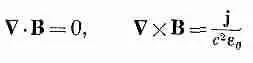Feynmann - Feynmann 5b

(13.34)

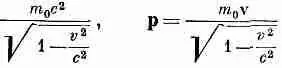
Далее, мы знаем, что энергия U и импульс частицы р, движущейся со скоростью v, даются выражениями

где m 0 — ее масса покоя. Мы знаем также, что U и р обра­зуют релятивистский четырехвектор. Поскольку r и j зави­сят от скорости v в точности, как U и р, то можно заклю­чить, что r и j также компоненты релятивистского четырехвектора. Это свойство есть ключ к общему анализу поля проволоки, движущейся с любой скоростью, и мы могли бы его использовать, если бы захотели решить снова задачу со скоростью частицы v 0, не равной скорости электронов про­водимости.

Если нам нужно перевести r и j в систему координат, движущуюся со скоростью и в направлении х, то мы знаем, что они преобразуются в точности как t и (х, у, z ); поэтому мы имеем (см. вып. 2, гл. 15)

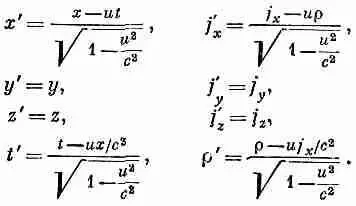
(13.35)

С помощью этих уравнений можно связать заряды и токи в одной системе с зарядами и токами в другой. Взяв заряды и токи в какой-то системе, можно решить электромагнитную задачу в этой системе, пользуясь уравнениями Максвелла. Результат, который мы получим для движения частиц, будет одним и тем же, независимо от выбранной системы отсчета. Позже мы вернемся к релятивистским преобразованиям элек­тромагнитных полей.

§ 8. Суперпозиция; правило правой руки

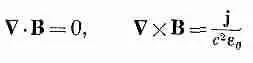
Мы закончим эту главу еще двумя замечаниями по вопро­сам магнитостатики. Первое: наши основные уравнения для магнитного поля

линейны до В и j. Это означает, что принцип суперпозиции (наложения) приложим и к магнитному полю. Поле, создава­емое двумя разными постоянными токами, есть сумма собствен­ных полей от каждого тока, действующего по отдельности. Наше второе замечание относится к правилам правой руки, с которыми мы уже сталкивались (правило правой руки для магнитного поля, создаваемого током). Мы указывали также, что намагничивание железного магнита объясняется вращением электронов в материале. Направление магнитного поля вра­щающегося электрона связано с осью его вращения тем же самым правилом правой руки. Поскольку В определяется правилом определенной руки (с помощью либо векторного произведения, либо ротора), он называется аксиальным век­тором. (Векторы, направление которых в пространстве не за­висит от ссылок на левую или правую руку, называются по­лярными векторами. Например, смещение, скорость, сила и Е — полярные векторы.)

Физически наблюдаемые величины в электромагнетизме, однако, не связаны с правой или левой рукой. Из гл. 52 (вып. 4) мы знаем, что электромагнитные взаимодействия симметричны по отношению к отражению. При вычислении магнитных сил между двумя наборами токов результат всегда инвариантен по отношению к перемене рук. Наши уравнения, независимо от условия правой руки, приводят к конечному результату, что параллельные токи притягиваются, а противоположные — отталкиваются. (Попробуйте вычислить силу с помощью «пра­вила левой руки».) Притяжение или отталкивание есть поляр­ный вектор. Так получается потому, что при описании любого полного взаимодействия мы пользуемся правилом правой руки дважды — один раз, чтобы найти В из токов, а затем, чтобы найти силу, оказываемую полем В на второй ток. Два раза пользоваться правилом правой руки — все равно что два раза пользоваться правилом левой руки. Если бы мы условились перейти к системе левой руки, все наши поля В изменили бы знак, но все силы или (что, пожалуй, нагляднее) наблюдаемые ускорения объектов не изменились бы.

Хотя физики недавно, к своему удивлению, обнаружили, что не все законы природы всегда инвариантны по отношению к зеркальным отражениям, тем не менее законы электромаг­нетизма обладают этой фундаментальной симметрией.

* Или, короче,─ тесла. ─ прим. ред.

*Потом мы увидим, что такие предположения, вообще говоря, неправильны для электромагнитных сил!

* Это и есть магнитная проницаемость пустоты.

Глава 14

МАГНИТНОЕ ПОЛЕ В РАЗНЫХ СЛУЧАЯХ

§1.Векторный потенциал