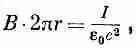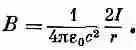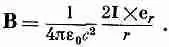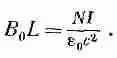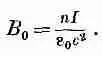Feynmann - Feynmann 5b

Полный ток через петлю есть просто ток I в проводе, поэтому

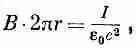
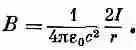
или

(13.17)

Напряженность магнитного доля спадает обратно пропорцио­нально r, расстоянию от оси провода. При желании уравнение (13.17) можно записать в векторной форме. Вспоминая, что В направлено перпендикулярно как I, так и r, имеем

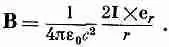
(13.18)

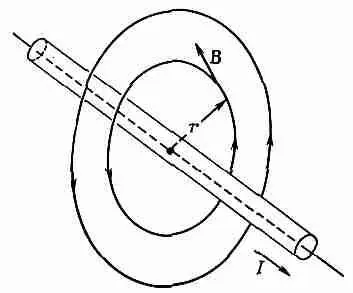
Фиг. 13.7. Магнитное поле вне длинного провода с током I .

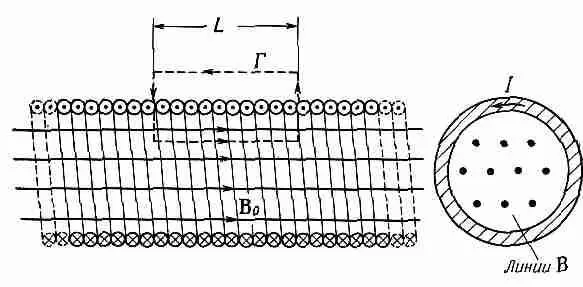
Фиг. 13.8. Магнитное поле длинного соленоида.

Мы выделили множитель 1/4pe 0с 2, потому что он часто по­является. Стоит запомнить, что он равен в точности 10 -7(в си­стеме единиц СИ), потому что уравнение вида (13.17) исполь­зуется для определения единицы тока, ампера. На расстоянии 1 м ток в 1а создает магнитное поле, равное 2·10 -7 вебер/м 2 .

Раз ток создает магнитное поле, то он будет действовать с некоторой силой на соседний провод, по которому также про­ходит ток. В гл. 1 мы описывали простой опыт, показывающий силы между двумя проводами, по которым течет ток. Если про­вода параллельны, то каждый из них перпендикулярен полю В другого провода; тогда провода будут отталкиваться или при­тягиваться друг к другу. Когда токи текут в одну сторону, провода притягиваются, когда токи противоположно направле­ны,— они отталкиваются.

Возьмем другой пример, который тоже можно проанализи­ровать с помощью закона Ампера, если еще добавить кое-какие сведения о характере поля. Пусть имеется длинный провод, свернутый в тугую спираль, сечение которой показано на фиг. 13.8. Такая спираль называется соленоидом. На опыте мы наблюдаем, что когда длина соленоида очень велика по сравнению с диаметром, то поле вне его очень мало по сравне­нию с полем внутри. Используя только этот факт и закон Ам­пера, можно найти величину поля внутри.

Поскольку поле остается внутри (и имеет нулевую дивер­генцию), его линии должны идти параллельно оси, как пока­зано на фиг. 13.8. Если это так, то мы можем использовать закон Ампера для прямоугольной «кривой» Г на рисунке. Эта кривая проходит расстояние L внутри соленоида, где поле, скажем, равно В 0 ,затем идет под прямым углом к полю и возвращается назад по внеш­ней области, где полем можно пренебречь.

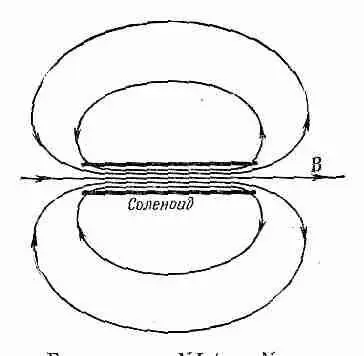
Фиг. 13.9. Магнитное поле вне соленоида.

Линей­ный интеграл от В вдоль этой кривой равен в точ­ности B 0 L , и это должно равняться 1/e 0с 2, умноженному на полный ток внутри Г, т. е. на N I (где N — число витков соленоида на длине L ). Мы имеем

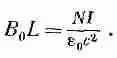
Или же, вводя n — число витков на единицу длины соленоида (так что n = N / L ), мы получаем

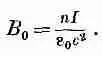
(13.19)

Что происходит с линиями В, когда они доходят до конца соленоида? По-видимому, они как-то расходятся и возвращают­ся в соленоид с другого конца (фиг. 13.9). В точности такое же поле наблюдается вне магнитной палочки. Ну а что же такое магнит? Наши уравнения говорят, что поле В возникает от присутствия токов. А мы знаем, что обычные железные бруски (не батареи и не генераторы) тоже создают магнитные поля. Вы могли бы ожидать, что в правой части (13.12) или (13.13) должны были бы быть другие члены, представляющие «плот­ность намагниченного железа» или какую-нибудь подобную величину. Но такого члена нет. Наша теория говорит, что магнитные эффекты железа возникают от каких-то внутренних токов, уже учтенных членом j.

Вещество устроено очень сложно, если рассматривать его с глубокой точки зрения; в этом мы уже убедились, когда пы­тались понять диэлектрики. Чтобы не прерывать нашего из­ложения, отложим подробное обсуждение внутреннего меха­низма магнитных материалов типа железа. Пока придется принять, что любой магнетизм возникает за счет токов и что в постоянном магните имеются постоянные внутренние токи. В случае железа эти токи создаются электронами, вращающи­мися вокруг собственных осей. Каждый электрон имеет такой спин, который соответствует крошечному циркулирующему току. Один электрон, конечно, не дает большого магнитного поля, но в обычном куске вещества содержатся миллиарды и миллиарды электронов. Обычно они вращаются любым образом, так что суммарный эффект исчезает. Удивительно то, что в немногих веществах, подобных железу, большая часть элек­тронов крутится вокруг осей, направленных в одну сторону,— у железа два электрона из каждого атома принимают участие в этом совместном движении. В магните имеется большое число электронов, вращающихся в одном направлении, и, как мы увидим, их суммарный эффект эквивалентен току, циркули­рующему по поверхности магнита. (Это очень похоже на то, что мы нашли в диэлектриках,— однородно поляризованный диэлектрик эквивалентен распределению зарядов на его по­верхности.) Поэтому не случайно, что магнитная палочка эк­вивалентна соленоиду.