Feynmann - Feynmann 5b

Для кристаллов, не обладающих постоянным моментом, можно развить теорию диэлектрической проницаемости, куда включается электронная поляризуемость атомов. Делается это почти так же, как для жидкостей. Некоторые кристаллы имеют внутренние моменты, и вращение их также вносит вклад в x. В ионных кристаллах, таких, как NaCl, возникает также ионная поляризуемость. Кристалл состоит из положительных и отрицательных ионов, расположенных в шахматном порядке, и в электрическом поле положительные ионы тянутся в одну сторону, а отрицательные — в другую; возникает результи­рующее смещение положительных и отрицательных зарядов, а следовательно, и объемная поляризация. Мы могли бы оце­нить величину ионной поляризуемости, зная жесткость кри­сталлов соли, но мы не будем сейчас останавливаться на этом вопросе.

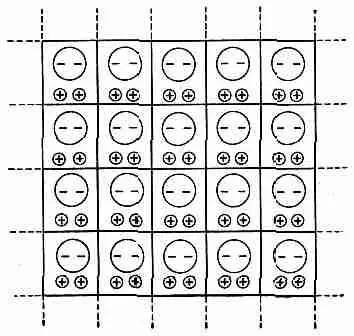
Фиг. 11.8. Сложная кристаллическая решетка может иметь постоянную внутреннюю поля­ризацию Р.

§ 7. Сегиетоэлектричество; титанат бария

Мы опишем здесь особый класс кристаллов, которые, можно сказать, почти случайно обладают «встроенным» постоянным электрическим моментом. Ситуация здесь настолько критична, что, если слегка увеличить температуру выше некоторой, кри­сталл этого класса совсем потеряет постоянный момент. С дру­гой стороны, если структура кристалла близка к кубической, так что электрические моменты могут располагаться в разных направлениях, можно обнаружить большие изменения полного момента при изменении приложенного электрического поля. Все моменты перевертываются в направлении поля, и мы полу­чаем большой эффект. Вещества, обладающие такого рода постоянным моментом, называются сегнетоэлектриками. Мы хотели бы объяснить механизм сегнетоэлектричества на частном примере какого-нибудь сегнетоэлектрического ма­териала. Сегнетоэлектрические свойства могут возникать нес­колькими путями; однако мы разберем только один из них на примере таинственного титаната бария (BaТiO 3). Это вещество обладает кристаллической решеткой, основная ячейка кото­рого изображена на фиг. 11.9. Оказывается, что выше некоторой температуры (а именно 118°С) титанат бария — обычный ди­электрик с огромной диэлектрической проницаемостью, а ниже этой температуры он неожиданно приобретает постоянный момент.

При вычислении поляризации твердых тел мы должны сна­чала найти локальные поля в каждой элементарной ячейке. Причем для этого нужно ввести поля самой поляризации, как это делалось в случае жидкости. Но кристалл — не однородная жидкость, так что мы не можем взять в качестве локального поля то, что мы нашли в сферической дыре. Если мы сделаем это для кристалла, то окажется, что множитель 1/ 3в уравнении (11.24) слегка изменится, но ненамного. (Для простого куби­ческого кристалла он равен в точности 1/ 3.) Поэтому предпо­ложим в нашем предварительном обсуждении, что этот множитель для BaTi0 3действительно равен 1/ 3.

Далее, когда мы писали уравнение (11.28), вам, наверное, было интересно знать, что случится, если N a станет больше 3. На первый взгляд величина x должна бы стать отрицательной. Но такого наверняка не может быть. Посмотрим, что произойдет, если в каком-нибудь определенном кристалле постепенно увеличивать значение a.

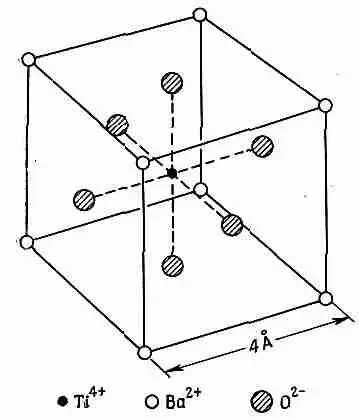
Фиг. 11.9. Элементарная ячей­ка ВаТ iO 3 .

Атомы в действительности запол­няют большую часть пространства; показаны только положения их центров.

По мере роста a растет и поляризация, создавая большее локаль­ное поле. Но увеличившее­ся локальное поле заполяризует атом еще больше, дополнительно усиливая само локальное поле. Если атомы достаточно «податливы», про­цесс продолжается; возникает своего рода обратная связь, приводящая к безудержному росту поляризации (если пред­положить, что поляризация каждого атома увеличивается пропорционально полю). Условие «разгона» возникает при N a = 3. Поляризация, конечно, не обращается в бесконечность, потому что при сильных полях пропорциональность между индуцированным моментом и электрическим полем нарушается, так что наши формулы становятся неправильными. А полу­чается то, что в решетку, оказывается, «встроена» большая внутренняя самопроизвольная поляризация.