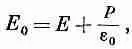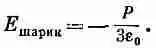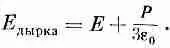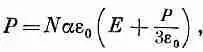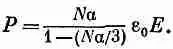Вы можете подумать, что «средний» атом в «среднем» положении почувствует именно это среднее поле. Но все не так просто, и в этом можно убедиться, представив, что в диэлектрике имеются отверстия разной формы. Предположим, что мы вырезали в поляризованном диэлектрике щель, ориентированную параллельно полю (фиг. 11.5, а). Поскольку мы знаем, что СXE = 0, то линейный интеграл от Е вдоль кривой Г, направленной так, как показано на фиг. 11.5, б, должен быть равен нулю. Поле внутри щели должно давать такой вклад, который в точности погасит вклад от поля вне щели. Поэтому поле E 0в центре длинной тонкой щели равно Е, т.е. среднему электрическому полю, найденному в диэлектрике.
Рассмотрим теперь другую щель, повернутую своей широкой стороной перпендикулярно Е (фиг. 11.5, в). В этом случае поле e 0в щели не совпадает с Е, потому что на стенках щели возникают поляризационные заряды. Применив закон Гаусса к поверхности S, изображенной на фиг. 11.5, г, мы находим, что поле Е йвнутри щели дается выражением
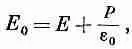
(11.22)
где Е, как и раньше,— электрическое поле в диэлектрике. (Гауссова поверхность охватывает поверхностный поляризационный заряд s пол= Р.) Мы отмечали в гл. 10, что e 0 Е + Р часто обозначают через D , поэтому e 0Е 0= D 0 равно величине D в диэлектрике.
В ранний период истории физики, когда считалось очень важным определять каждую величину прямым экспериментом, физики были очень довольны, обнаружив, что они могут определить то, что понимают под Е и D в диэлектрике, не ползая в промежутках между атомами. Среднее поле Е численно равно полю Е 0, измеренному в щели, параллельной полю. А поле D могло быть измерено с помощью Е 0 , найденной в щели, перпендикулярной полю. Но никто эти поля никогда не измерял (таким способом, во всяком случае), так что это одна из многих бесплодных проблем.
В большинстве жидкостей, не слишком сложных по своему строению, каждый атом в среднем так окружен другими атомами, что можно с хорошей точностью считать его находящимся в сферической полости. И тогда мы спросим: «Чему равно поле в сферической полости?» Мы замечаем, что вырезание сферической дырки в однородном поляризованном диэлектрике равносильно отбрасыванию шарика из поляризованного материала, так что мы можем ответить на этот вопрос. (Мы должны представить себе, что поляризация была «заморожена» до того, как мы вырезали дырку.) Однако в силу принципа суперпозиции поле внутри диэлектрика, до того как оттуда был вынут шарик, есть сумма полей от всех зарядов вне объема шарика плюс полей от зарядов внутри поляризованного шарика.
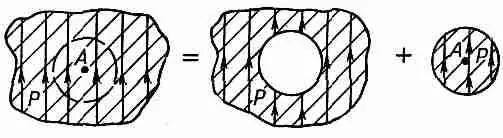
Фиг. 11.6. Поле в любой точке А диэлектрика можно представить в виде суммы поля сферической дырки и поля сферического вкладыша.
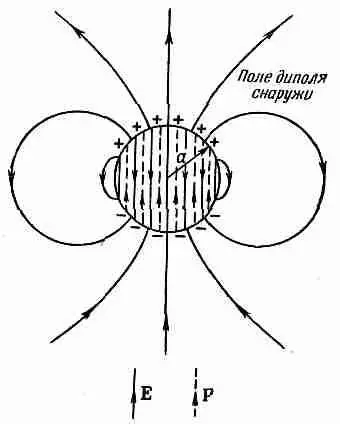
Фиг. 11.7. Электрическое поле однородно поляризованного шарика.
Следовательно, если поле внутри однородного диэлектрика мы назовем Е, то можно записать
E=E дырка+E шарнк,
(11.23)
где E дырка— поле в дырке, а E шарик— поле в однородно поляризованном шарике (фиг. 11.6). Поле однородно поляризованного шарика показано на фиг. 11.7. Электрическое поле внутри шарика однородно и равно
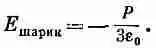
(11.24)
С помощью (11.23) получаем
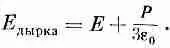
(11.25)
Поле в сферической полости больше среднего поляна величину Р/Зe 0. (Сферическая дырка дает поле, находящееся на 1/ 3пути от поля параллельной щели к полю перпендикулярной щели.)
§ 5. Диэлектрическая проницаемость жидкостей; формула Клаузиуса — Моссотти
В жидкости мы ожидаем, что поле, поляризующее отдельный атом, скорее похоже на Е дырка, чем просто на Е. Если взять E дыркаиз (11.25) в качестве поляризующего поля, входящего в (11.6), то уравнение (11.8) приобретет вид
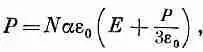
(11.26)
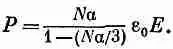
Читать дальше