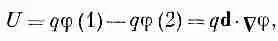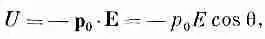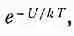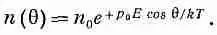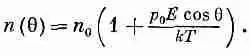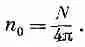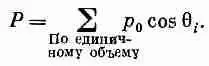Feynmann - Feynmann 5b

§ 3. Полярные молекулы; ориентационная поляризация

Теперь рассмотрим молекулу, обладающую постоянным дипольным моментом р 0 , например молекулу воды. В отсутст­вие электрического поля отдельные диполи смотрят в разных направлениях, так что суммарный момент в единице объема равен нулю. Но если приложить электрическое поле, то сразу же происходят две вещи: во-первых, индуцируется добавочный дипольный момент из-за сил, действующих на электроны; эта часть приводит к той же самой электронной поляризуемости, которую мы нашли для неполярной молекулы. При очень точ­ном исследовании этот эффект, конечно, нужно учитывать, но мы пока пренебрежем им. (Его всегда можно добавить в конце.) Во-вторых, электрическое поле стремится выстроить отдельные диполи, создавая результирующий момент в единице объема.

Фиг. 11.2. В газе полярных молекул отдельные моменты ориен­тированы случайным образом, средний момент в небольшом объеме равен нулю (а); под действием электрического поля в среднем возникает некоторое выстраивание молекул (б).

Если бы в газе выстроились все диполи, поляризация была бы очень большой, но этого не происходит. При обычных темпе­ратурах и напряженностях поля столкновения молекул при их тепловом движении не позволяют им как следует выстроить­ся. Но некоторое выстраивание все же происходит, а отсюда и небольшая поляризация (фиг. 11.2). Возникающая поляри­зация может быть подсчитана методами статистической меха­ники, описанными в гл. 40 (вып. 4).

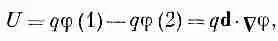
Чтобы использовать этот метод, нужно знать энергию диполя в электрическом поле. Рассмотрим диполь с моментом р 0в электрическом поле (фиг. 11.3). Энергия положительного за­ряда равна qj (1), а энергия отрицательного есть —qj (2). Отсюда получаем энергию диполя

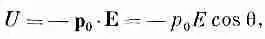
или

(11.14)

где q — угол между р 0и Е. Как и следовало ожидать, энергия становится меньше, когда диполи выстраиваются вдоль поля. Теперь с помощью методов статистической механики мы выясним, насколько сильно диполи выстраиваются. В гл. 40 (вып. 4) мы нашли, что в состоянии теплового равновесия относительное число молекул с потенциальной энергией U пропорционально

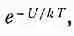
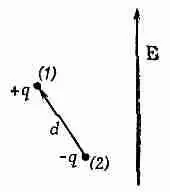
(11.15)

Фие. 11.3. Энергия диполя р 0 в поле Е равна —р 0·Е.

где U (х, у, z ) — потенциальная энергия как функция поло­жения. Оперируя теми же аргументами, можно сказать, что если потенциальная энергия как функция угла имеет вид (11.14), то число молекул под углом 0, приходящееся на единичный телесный угол, пропорционально ехр (— U / kT ).

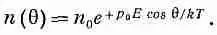
Полагая число молекул на единичный телесный угол, на­правленных под углом q, равным n (q), имеем

(11.16)

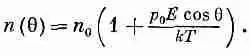
Для обычных температур и полей показатель экспоненты мал, и, разлагая экспоненту, можно воспользоваться прибли­женным выражением

(11.17)

Найдем n , проинтегрировав (11.17) по всем углам; результат должен быть равен N , т.е. числу молекул в единице объема. Среднее значение cos q при интегрировании по всем углам есть нуль, так что интеграл равен просто n 0 , умноженному на полный телесный угол 4p. Получаем

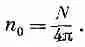
(11.18)

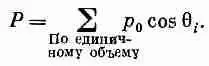
Из (11.17) видно, что вдоль поля (cosq=1) будет ориен­тировано больше молекул, чем против поля (cosq = -1). Поэтому в любом малом объеме, содержащем много молекул, возникнет суммарный дипольный момент на единицу объема, т.е. поляризация Р. Чтобы вычислить Р, нужно знать векторную сумму всех молекулярных моментов в единице объема. Мы зна­ем, что результат будет направлен вдоль Е, поэтому нужно только просуммировать компоненты в этом направлении (ком­поненты, перпендикулярные Е, при суммировании дадут нуль):