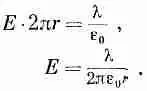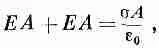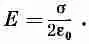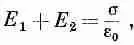Feynmann - Feynmann 5a

Фиг. 5.5. Цилиндрическая гауссо­ва поверхность, коаксиальная за­ряженной прямой.

1 — гауссова поверхность; 2 — заря­женная прямая.

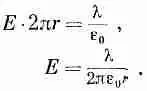
(Может быть, это нелегко доказать, но это верно, если пространство симметрично, а мы считаем, что это так.) Применить закон Гаусса можно следующим образом. Вооб­разим себе поверхность, имеющую форму цилиндра, ось ко­торого совпадает с нашей прямой (фиг. 5.5). Согласно закону Гаусса, весь поток Е из этой поверхности равен заряду внутри нее, деленному на e 0. Раз поле считается нормальным к поверх­ности, то его нормальная составляющая — это величина векто­ра поля. Обозначим ее Е. Пусть радиус цилиндра будет r, а длина его для удобства выбрана равной единице. Поток сквозь цилиндрическую поверхность равен произведению Е на площадь поверхности, т. е. на 2pr. Поток через торцы равен нулю, потому что поле касательно к ним. Весь заряд внутри нашей поверх­ности равен как раз l, потому что длина оси цилиндра равна единице. Тогда закон Гаусса дает

(5.2)

Электрическое поле заряженной прямой обратно пропорцио­нально первой степени расстояния от прямой.

§ 6. Заряженная плоскость; пара плоскостей

В качестве другого примера рассчитаем поле однородно заряженного плоского листа. Предположим, что лист имеет бесконечную протяженность и заряд на единицу площади равен а. Сразу приходит в голову следующее соображение: из симмет­рии следует, что поле направлено всюду поперек плоскости, и если не существует поля от всех прочих зарядов в мире, то поля по обе стороны плоскости должны совпадать (по величине). На этот раз за гауссову поверхность мы примем прямоугольный ящик, пересекающий нашу плоскость (фиг. 5.6). Каждая из граней, параллельных плоскости, имеет площадь А. Поле нор­мально к этим двум граням и параллельно остальным четырем. Суммарный поток равен Е, умноженному на площадь первой грани, плюс Е, умноженному на площадь противоположной грани; от остальных граней никаких слагаемых

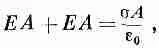
не войдет. За­ряд внутри ящика равен s А. Уравнивая поток с зарядом, на­пишем

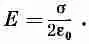
откуда

(5.3)

Простой, но важный результат.

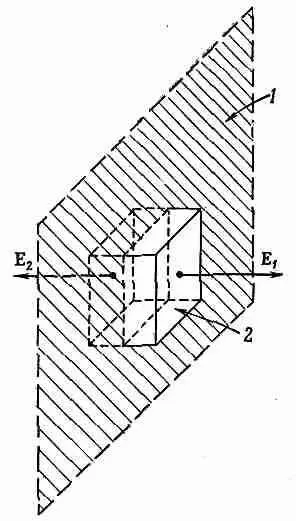
Фиг. 5.6. Электрическое поле во­зле однородно заряженной плоско­сти, найденное с помощью теоремы Гаусса, применяемой к воображае­мому ящику.

1 — однородно заряженная плоскость;

2 — гауссова поверхность.

Вы помните, может быть, что тот же результат был получен в первых главах интегрирова­нием по всей плоскости. Закон Гаусса дает ответ намного бы­стрее (хотя он не так широко применим, как прежний метод).

Подчеркнем, что этот резуль­тат относится только к полю,

созданному зарядами, размещенными на плоскости. Если по соседству есть другие заряды, общее поле близ плоскости бы­ло бы суммой (5.3) и поля прочих зарядов. Закон Гаусса тогда только гарантировал бы, что

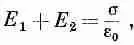
(5.4)

где E 1 и Е 2 — поля, направленные на каждой стороне плоско­сти наружу от нее.

Задача о двух параллельных плоскостях с равными и про­тивоположными плотностями зарядов +s и -s решается тоже просто, если только снова предположить, что внешний мир абсолютно симметричен. Составите ли вы суперпозицию двух ре­шений для отдельных плоскостей или построите гауссов ящик, охватывающий обе плоскости, в обоих случаях легко видеть, что поле снаружи плоскостей равно нулю (фиг. 5.7, а). Но, зак­лючив в ящик только одну или только другую поверхность, как показано на фиг. 5.7, б или в, мы легко обнаружим, что поле между плоскостями должно быть вдвое больше поля отдельной плоскости.

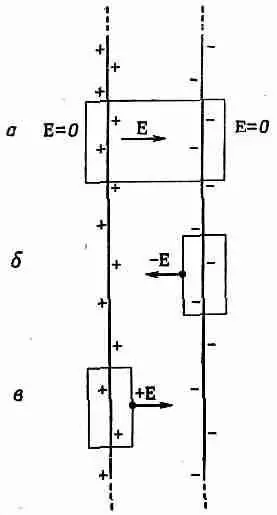
Фиг . 5.7. Поле между двумя за­ряженными листами равно s/e 0.

Итог таков:

(5.5)

Е (снаружи) =0. (5.6)

§ 7. Однородно заряженный шар; заряженная сфера