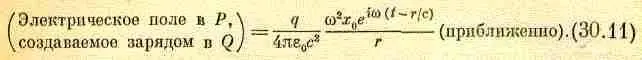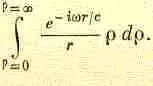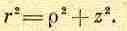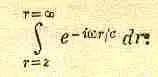Feynmann - Feynmann 3

В этой главе мы вычисляли интенсивность в разных направ­лениях при различном расположении источников. В заключение выведем формулу, которая нам понадобится в следующей гла­ве, посвященной показателю преломления. До сих пор мы об­ходились только относительными интенсивностями, а на этот раз мы получим формулу для полной величины поля при усло­виях, о которых будет рассказано ниже.

§ 7. Поле системы осцилляторов, расположенных на плоскости

Предположим, что имеется некоторая плоскость, которую за­полняют осцилляторы, причем все они колеблются в плоскости одновременно, с одной амплитудой и фазой. Чему равно поле на конечном, но достаточно большом расстоянии от плоскости? (Мы не можем выбрать точку наблюдения очень близко от плос­кости, потому что у нас нет точных формул для поля вблизи источников.) Пусть плоскость зарядов совпадает с плоскостью XY и нас интересует поле в точке Р, лежащей на оси z, достаточ­но далеко от плоскости (фиг. 30.10). Предположим, что число зарядов на единичной площадке равно n, а величина каждого заряда д. Все заряды совершают одинаковые гармонические колебания в одном и том же направлении, с той же амплитудой и фазой. Смещение заряда из его среднего положения описы­вается функцией x 0coswt. Вводя комплексную амплитуду, действительная часть которой дает реальное движение, будем описывать колебание заряда функцией x 0e i w t.

Чтобы найти поле, создаваемое всеми зарядами в точке Р, нужно вычислить сначала поле отдельного заряда q, а затем сложить поля всех зарядов. Как известно, поле излучения про­порционально ускорению заряда, т. е.. — w 2x 0е i w t(и одинаково для всех зарядов). Электрическое поле в точке Р, создаваемое зарядом в точке Q, пропорционально ускорению заряда q, нужно только помнить, что поле в точке Р в момент времени t определяется ускорением заряда в более ранний момент времени t' =t-r/c, где r/c — время, за которое волна проходит расстояние от Q до Р. Поэтому поле в точке Р пропорционально

(30.10)

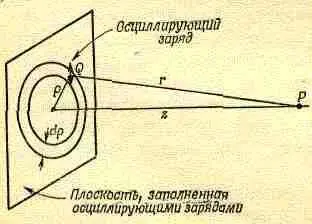
Фиг. 30 . 10. Поле излучения ос­циллирующих зарядов, заполняю­щих плоскость.

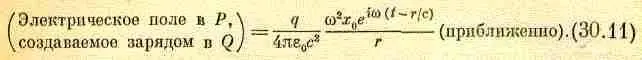
Подставляя это значение ускорения в формулу для поля, соз­даваемого зарядом на большом расстоянии, получаем

Однако эта формула не совсем правильна, поскольку нужно брать не все ускорение целиком, а его компоненту, перпендику­лярную линии QP . Мы предположим, однако, что точка Р нахо­дится от плоскости намного дальше, чем точка Q от оси z (рас­стояние r на фиг. 30.10), так что для эффектов, которые мы хо­тим учесть, косинус можно заменить единицей (косинус и так довольно близок к единице).

Полное поле в точке Р получается суммированием вкладов от всех зарядов в плоскости. Разумеется, мы должны взять векторную сумму полей. Но поскольку направление поля при­мерно одинаково для всех зарядов, в рамках сделанного прибли­жения достаточно сложить величины всех полей. Кроме того, в нашем приближении поле в точке Р зависит только от r, сле­довательно, все заряды с одинаковым r создают равные поля. Поэтому, прежде всего, сложим поля всех зарядов в кольце ши­риной dr и радиусом r. Интегрируя затем по всем r, получаем полное поле всех зарядов.

Число зарядов в кольце равно произведению площади кольца, 2nrdr, на h — плотность зарядов на единицу площади. Отсюда

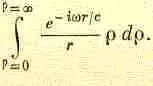
Интеграл берется в пределах r=0 и r=Ґ. Время t , конечно, зафиксировано, так что единственными меняющимися величинами являются r и r. Отвлечемся пока от постоянных множителей, включая и e i w t , и вычислим интеграл

(30.13)

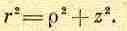
Для этого учтем соотношение между r и r :

(30.14)

При дифференцировании формулы (30.14) z нужно считать независимым от r, тогда

2rdr = 2rdr,

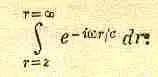
что очень кстати, поскольку при замене в интеграле rdr на r dr знаменатель r сокращается. Интеграл приобретает более простой вид