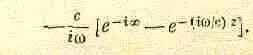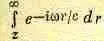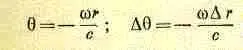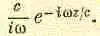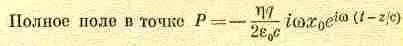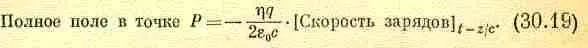Feynmann - Feynmann 3

(30.15)

. Экспонента интегрируется очень просто. Нужно поставить в знаменатель коэффициент при r в показателе экспоненты и взять саму экспоненту в точках, соответствующих пределам. Но пределы по r отличаются от пределов по р. Когда r=0, нижний предел r=z , т. е. пределы по r равны z и бесконечности. Ин­теграл (30.15) равен

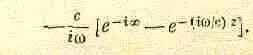
(30.16)

Вместо (r/с ) Ґ мы здесь написали Ґ, поскольку и то и другое означает просто сколь угодно большую величину!

А вот е - i Ґ— величина загадочная. Ее действительная часть, равная cos (-Ґ), с математической точки зрения величина со­вершенно неопределенная. [Хотя можно допустить, что она на­ходится где-то [а может быть и всюду (?)—между +1 и -1!]Но в физической ситуации эта величина может означать нечто вполне разумное и обычно оказывается равной нулю. Чтобы убедиться, что это так в нашем случае, вернемся к первоначальному инте­гралу (30.15)

Выражение (30.15) можно понимать как сумму большого числа маленьких комплексных чисел, модуль которых ar, a угол в комплексной плоскости q=-wr/с. Попробуем оценить эту сумму графически. На фиг. 30.11 отложены первые пять членов суммы. Каждый отрезок кривой имеет длину Dr и рас­положен под углом Dq =-w(Dr /с) к предыдущему отрезку. Сум­ма первых пяти слагаемых обозначена стрелкой из начальной точки к концу пятого отрезка. Продолжая прибавлять отрезки, мы опишем многоугольник, вернемся примерно к начальной точке и начнем описывать новый многоугольник. Чем большее число отрезков мы будем прибавлять, тем большее число раз мы обернемся, двигаясь почти по окружности с радиусом с/w. Теперь понятно, почему интеграл дает при вычислении неопре­деленный ответ!

Здесь мы должны обратиться к физическому смыслу нашего примера. В любой реальной ситуации плоскость зарядов не может быть бесконечной, а должна где-то оборваться. Если плоскость резко обрывается и ее граница имеет точно форму окружности, то наш интеграл будет равен некоторому значению на этой окружности (см. фиг. 30.11). Если же плотность зарядов

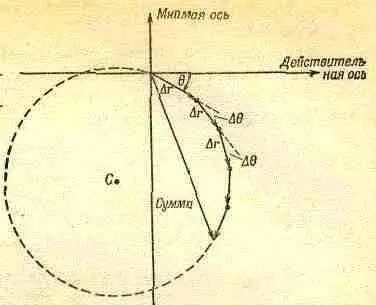
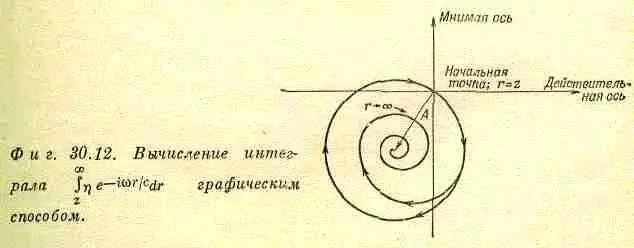
Фиг. 30.11. Вычисление интегра­ла

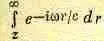
графическим способом.

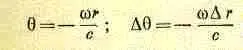
постепенно уменьшается по мере удаления от центра (или обра­щается в нуль вне некоторой границы неправильной формы, так что для достаточно больших r вклад всего кольца шириной dr равен нулю), то коэффициент ню в точном интеграле убывает, стремясь к нулю. Поскольку длина добавляемых отрезков в этом случае уменьшается, а угол Dq остается тем же самым, график кривой, соответствующей интегралу, будет иметь вид спирали. Спираль оканчивается в центре первоначальной ок­ружности, как изображено на фиг. 30.12. Физически правиль­ное значение интеграла дается величиной А, которой на схеме соответствует расстояние от начальной точки до центра окруж­ности, равное как нетрудно убедиться.

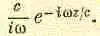
(30.17)

Точно такой же результат мы получили бы из (30.16), положив e - i Ґ=0.

(Есть еще одна причина, почему вклад в интеграл от больших значений r стремится к нулю,— это опущенный нами множитель, учитывающий проекцию ускорения на плоскость, перпендику­лярную линии PQ.)

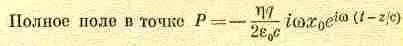
Нас, конечно, интересует именно случай, имеющий физи­ческий смысл, поэтому мы положим е - i Ґ равным нулю. Возвраща­ясь к формуле (30.12) для поля и вводя все опущенные ранее множители, мы получаем

(30.18)

(помня, что l/i =-i).

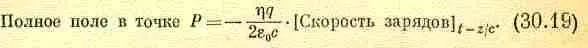
Интересно отметить, что i w x 0 e i w t в точности равно скорости зарядов, так что выражения для поля можно переписать в виде

Этот результат немного странен, потому что запаздывание отве­чает расстоянию z, которое есть кратчайшее расстояние от Р до плоскости. Но таков ответ, и, к счастью, формула довольно проста. [Добавим кстати, что, хотя формулы (30.18) и (30.19) бы­ли получены только для достаточно большого расстояния от плоскости, обе они оказываются правильными для любых z,