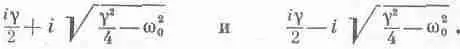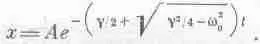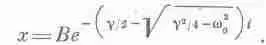Feynmann - Feynmann 2a

Значит, наши колебания — это колебания с фазовым сдвигом и, как полагается, с затуханием.

§ 3. Переходные колебания в электрических цепях

Посмотрим, как выглядят переходные колебания. Для этого соберем цепь, изображенную на фиг. 24.2.

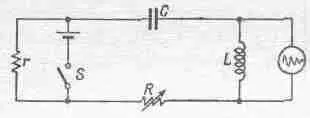
Фиг. 24,2. Электрическая цепь для демонстраций переходных колебаний.

В этой цепи разность потенциалов между концами индуктивности L поступает в осцил­лоскоп. Неожиданное включение рубильника S включает допол­нительное напряжение и вызывает в осцилляторной цепи переходные колебания. Эти колебания аналогичны колебаниям механического осциллятора, вызванными неожиданным ударом. Сама цепь представляет собой электрический аналог механи­ческого осциллятора с затуханием, и мы можем наблюдать коле­бания при помощи осциллоскопа. Он покажет нам кривые, анализом которых мы и займемся. На фиг. 24.3—24.6 представ­лены кривые затухающих колебаний, полученные на экране осциллоскопа. На фиг. 24.3 показаны затухающие колебания в цепи с большой Q , т. е. с малым значением g .

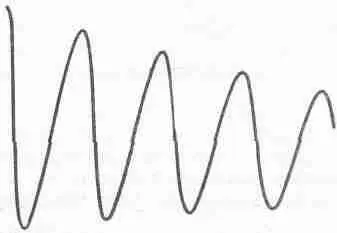
Фиг. 24.3. Затухающие коле­бания.

В такой цепи ко­лебания затухают не очень быстро; мы видим довольно длинную синусоиду с медленно убывающим размахом.

Теперь давайте посмотрим, что произойдет, если мы будем уменьшать Q , так что колебания должны затухать быстрее. Чтобы уменьшить Q , увеличим сопротивление цепи R . При повороте ручки сопротивления колебания действительно зату­хают скорее (фиг. 24.4).

Фиг. 24.4. Колебания затухают быстрее.

Если еще увеличить сопротивление, то колебания затухнут еще быстрее (фиг. 24.5).

Фиг, 24.5. Колебания почти исчезли.

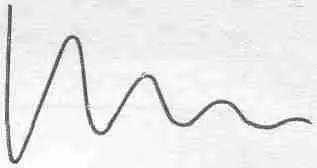
Но если сопротив­ление увеличить сверх некоторого предела, колебаний мы вооб­ще не увидим. А может быть, нам просто отказывают глаза? Увеличим еще сопротивление и получим тогда кривую, пред­ставленную на фиг. 24.6; по ней можно лишь с натяжкой сказать, что в цепи произошли колебания, ну разве что одно.

Фиг. 24.6. Колебаний нет.

Можем ли мы математически объяснить это явление?

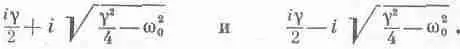
Сопротивление механического осциллятора, конечно, про­порционально g. В нашем случае g — это R / L . Теперь, если уве­личивать g, то в столь приятных нам решениях (24.14) и (24.15) наступает беспорядок; когда g /2 становится больше w 0, реше­ния приходится записывать по-другому:

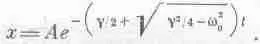
Это снова два решения, которые приводят нас к решениям exp(ia 1t) и ехр(ia 2t). Подставив теперь a 1, получим

Никаких колебаний. Чисто экспоненциальное убывание. То же самое дает и второе решение

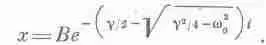
Заметим, что квадратный корень не может превысить g/2; даже если w 0=0, оба члена равны. Если же w 2 0отличается от g/ 2/4, то квадратный корень меньше g//2 и выражение в круглых скобках всегда положительно. Это очень хорошо! Почему? Да потому что если бы это выражение было отрицательным, то е пришлось бы возводить в положительную степень и мы по­лучили бы возрастающее со временем решение. Но при увели­чении в цепи сопротивления колебания не могут возрастать, зна­чит, мы избегли противоречия. Итак, мы получили два решения; оба решения экспоненциально затухают, но одно из них стре­мится «умереть» гораздо скорее. Общее решение, конечно, пред­ставляет собой комбинацию обоих решений, а значения коэф­фициентов А и В зависят от того, как начинаются колебания, каковы начальные условия. В нашей цепи случилось так, что А — отрицательное число, а В — положительное, поэтому на экране осциллоскопа мы увидели разность двух экспонент.