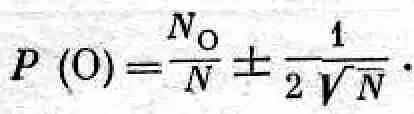Feynmann - Feynmann 1

На фиг. 6.6 отложены числа N O / N для тех подбрасываний монеты, о которых мы говорили раньше.

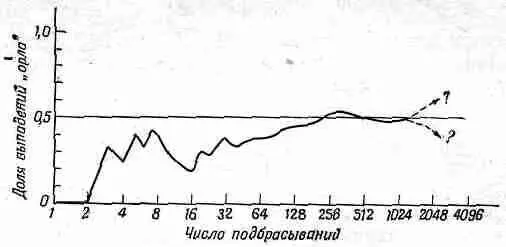
Фиг. 6.6. Доля выпадений «орла» в некоторой частной последовательности N подбрасываний монеты.

Как видите, при уве­личении числа N кривая все ближе и ближе подходит к 0,5. Но, к сожалению, нет никаких гарантий, что для каждой дан­ной серии или комбинации серий наблюдаемое отклонение будет близко к ожидаемому отклонению. Всегда есть конечная веро­ятность, что произойдет большая флуктуация — появление большого числа выпадений «орла» или «решки»,— которая даст произвольно большое отклонение. Единственное, что можно сказать,— это если отклонения близки к ожидаемому 1/ 2ЦN (скажем, со множителем 2 или 3), то нет оснований считать монету «поддельной» (или что партнер плутует).

Мы не рассматривали еще случаи, когда для монеты или ка­кого-то другого объекта испытания, подобного монете (в том смысле, что возможны два или несколько достоверно не пред­сказуемых исхода наблюдения, например камень, который мо­жет упасть только на какую-то из двух сторон), имеется дос­таточно оснований полагать, что вероятности разных исходов не равны. Мы определили вероятность Р( O ) как отношение o>/N. Но что принять за величину о>? Каким образом можно узнать, что ожидается? Во многих случаях самое луч­шее, что можно сделать, это подсчитать число выпадений «ор­ла» в большой серии испытаний и взять o> =N o(наблюден­ное). (Как можно ожидать чего-то еще?) При этом, однако, ну­жно понимать, что различные наблюдатели и различные серии испытаний могут дать другое значение P(О), отличное от нашего. Следует ожидать, однако, что все эти различные ответы не будут расходиться больше чем на 1/ 2ЦN [если Р(O) близко к половине], Физики-экспериментаторы обычно говорят, что «эксперимен­тально найденная» вероятность имеет «ошибку», и записывают это в виде

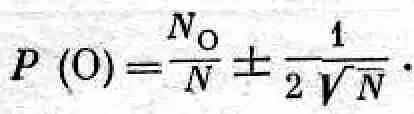
(6.14)

При такой записи подразумевается, что существует некая «ис­тинная» вероятность, которую в принципе можно подсчитать, но что различные флуктуации приводят к ошибке при экспери­ментальном ее определении. Однако нет возможности сделать эти рассуждения логически согласованными. Лучше все-таки, чтобы вы поняли, что вероятность в каком-то смысле — вещь субъективная, что она всегда основывается на какой-то неопре­деленности наших познаний и величина ее колеблется при их изменении.

§ 4. Распределение вероятностей

Давайте вернемся к проблеме случайных блужданий, но теперь уже с некоторым изменением. Пусть в дополнение к случайному выбору направления шага (+ или -) некоторым непредсказуемым образом меняется также и его длина, причем требуется выполнение одного-единственного условия, чтобы длина шага в среднем была равна единице. Эта задача уже боль­ше похожа на тепловое движение молекул в газе. Обозначим длину шага через S , которая, вообще говоря, может быть лю­бой, но наиболее часто будет принимать значения где-то «вбли­зи» единицы. Для большей определенности давайте положим 2>=1, или, что эквивалентно, S C - K= 1. Вывод выражения для 2> при этом останется тем же, за исключением того, что уравнение (6.8) изменится теперь следующим образом:

2 N>=2 N -1>+2>=2 N -1>+1. (6.15)

Так что, как и прежде,

2 N>=N. (6.16)

Каково же в этом случае будет распределение расстояний! Какова, например, вероятность того, что после 30 шагов D ока­жется равным нулю? Вероятность этого равна нулю! Вообще вероятность любой заданной величины D равна нулю. Действи­тельно, совершенно невероятно, чтобы сумма всех шагов назад (при произвольной длине каждого из них) в точности скомпенсировалась шагами вперед. В этом случае мы уже не можем построить график типа изображенного на фиг. 6.2.

Если же, однако, не требовать, чтобы D было в точности равно, скажем, нулю, или единице, или двум, а вместо этого говорить о вероятности получения D где-то вблизи нуля, или единицы, или двух, то при этом мы можем нарисовать график, подобный приведенному на фиг. 6.2. Назовем Р (х, Dx) вероятностью того, что D будет находиться где-то внутри интервала Dx в окрестности величины х (скажем, где-то между х и х +Dx). Если Ax достаточно мало, то вероятность того, что D попадет в этот интервал, должна быть пропорциональна его ширине, т. е. Ax. Поэтому мы можем утверждать, что