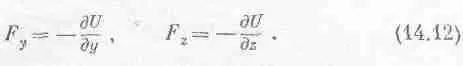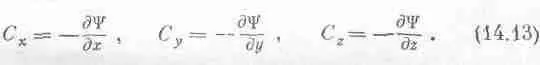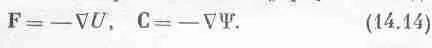Feynmann - Feynmann 1

В этих рассуждениях кроется ключ к вычислению силы или напряженности поля, когда потенциальная энергия известна.

Пусть потенциальная энергия тела в точке (х, у, z ) дана, а мы хотим узнать, какая сила действует на него в этой точке. Для этого нужно знать потенциал не только в этой точке, но и в соседних. Почему? Попробуем вычислить x-компоненту силы (если мы это сумеем сделать, то точно таким же способом мы вычислим и у- и z-компоненты, определив тем самым всю силу). Если б мы сдвинули тело на малое расстояние Dx, то работа, произведенная силой над телом, равнялась бы x-компоненте силы, умноженной на Dx (если Dx достаточно мало), и должна была бы быть равна изменению потенциальной энергии при переходе от одной точки к другой:

D W =- D U = F x Dx . (14.9)

Мы просто применили формулу ∫F·ds=-DU для очень

малых расстояний. Теперь разделим на Dx и обнаружим, что сила равна

F x=-DU/Dx. (14.10)

Конечно, это не совсем точно. На самом деле нам нужно перейти в (14.10) к пределу при Dx, стремящемся к нулю, потому что (14.10) точно соблюдается только для бесконечно малых Dx. Мы узнаем в правой части (14.10) производную U по х и хотим написать - dUldx . Но U зависит и от х, и от у, и от z, и для такого случая математики придумали другое обозначение, которое рас­считано на то, чтобы напоминать нам, что надо быть очень ос­торожным, дифференцируя такую функцию. Этот символ напо­минает, что только х считается изменяющимся, а у и z — нет. Вместо d они просто пишут «6 навыворот», или д. (По-моему, когда начинаешь изучать дифференциальные исчисления, то вообще лучше работать с д, а не с d ; d всегда хочется сократить, а вот на д как-то рука не поднимается!) Итак, они пишут dU / dx , а иногда в припадке строгости, желая быть очень бдительными, они ставят за дх скобку с маленькими у, z внизу ( dU / dx ) yz , что означает: «Продифференцируй U по х, считая у и z по­стоянными». Но мы чаще всего не будем отмечать, что осталось постоянным, из контекста это всегда можно понять. Но зато всегда будем писать д вместо d как предупреждение о том, что эта производная берется при постоянных значениях прочих переменных. Ее называют частной производной, т. е. производ­ной, для вычисления которой меняют часть переменных, х.

Итак, мы обнаруживаем, что сила в направлении х равна минус частной производной U по х:

F x =-д U / д x (14.11)

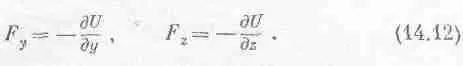
Точно так же и сила в направлении у получается дифференци­рованием U по у при постоянных х и z, а третья составляющая силы опять-таки есть производная по z при х и у постоянных:

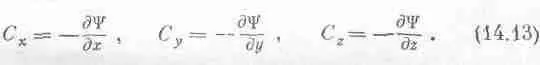
В этом и состоит способ получать силу из потенциальной энер­гии. Поле получается из потенциала в точности так же:

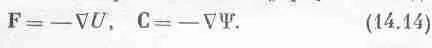
Заметим, кстати, что существует и другое обозначение (впро­чем, пока оно нам не понадобится). Так как Сесть вектор с компонентами х, у, z , то символы д/дх, д/ду, d / dz , дающие х-, у-, z-компоненты поля, чем-то напоминают векторы. Матема­тики изобрели знаменитый символ С, или grad, называемый «градиентом»; это не величина, а оператор, он делает из скаляра вектор. У него есть три составляющие: x-компонента этого grad есть д/дх, y-компонента — д/ду, а z-компонента— d / dz , и мы можем позабавиться, переписав наши формулы в виде

Глядя на С; мы мгновенно узнаем, что наши уравнения вектор­ные; но на самом деле уравнение (14.14) означает в точности то же, что и (14.11) и (14.12); просто это другой способ записи. Не желая писать каждый раз три уравнения, мы пишем одно лишь С U .

Еще один пример полей и потенциалов связан с электри­чеством. В этом случае сила, действующая на неподвижное тело, равна заряду, умноженному на поле: F= q Е. (В x-составляющую силы входят, вообще говоря, и члены, которые зависят от маг­нитного поля. Но из уравнения (12.10) легко увидеть, что сила, действующая на частицу со стороны магнитных полей, всегда направлена поперек поля и поперек ее скорости. Благодаря этому свойству магнетизм не производит никакой работы над движущимся зарядом, потому что сила перпендикулярна пере­мещению. Значит, вычисляя кинетическую энергию в электри­ческом и магнитном полях, можно пренебречь вкладом магнит­ного поля, так как оно не изменяет кинетической энергии.) По­ложим, что имеется только электрическое поле. Тогда мы можем рассчитать энергию или произведенную работу точно таким же способом, как и для тяготения: вычислить величину j, равную минус интегралу от Е· ds от произвольной фиксированной точки Р до точки, в которой вычисляется потенциал; тогда потенци­альная энергия в электрическом поле равна просто произведе­нию заряда на эту величину j: