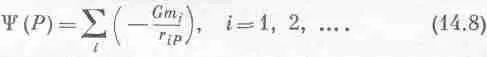Feynmann - Feynmann 1

Еще в одном случае может показаться, что энергия не сохраняется: когда мы изучаем часть всей системы. Вполне естественно, что если что-то взаимодействует с чем-то внешним и мы пренебрегаем этим взаимодействием, то теорема о сохра­нении энергии будет выглядеть неверной.

В классической физике в потенциальную энергию включались только тяготение и электричество, но теперь у нас есть и атом­ная энергия и многое другое. В классической теории, например, свет — это особая форма энергии, но можно, если нам этого хочется, представить себе энергию света как кинетическую энергию фотонов, и тогда наша формула (14.2) опять окажется справедливой.

§ 5. Потенциалы и поля

Теперь обратимся к некоторым идеям, связанным с потен­циальной энергией и с понятием поля. Пусть два больших тела А и В притягивают к себе третье малое тело с суммарной силой F. Мы уже отмечали в гл. 12, что сила притяжения частицы может быть представлена как произведение ее массы m на век­тор С, зависящий лишь от положения частицы:

F= m C.

Тяготение можно анализировать, считая, что в каждом месте пространства имеется вектор С, который «действует» на массу, помещенную в это место, но который присутствует там безот­носительно к тому, поместили ли мы туда массу или нет. Вектор Симеет три составляющие, и каждая из них является функцией от (х, y , z) — функцией положения в пространстве. Такую вещь мы называем полем и говорим, что тела А и В создают поле, т. е. «делают» вектор С. Когда тело помещено в поле, то сила дей­ствия на это тело равна его массе, умноженной на величину вектора поля в той точке, куда тело попало.

С потенциальной энергией можно сделать то же самое. Так как потенциальная энергия, интеграл от (Сила)·(ds), может быть записана в виде массы m, умноженной на интеграл от (Поле)·(ds) — это простое изменение масштаба, — то потен­циальную энергию U ( x , у, z) тела, расположенного в точке (х, у, z), можно записать как произведение m на другую функ­цию. Назовем ее потенциалом y . . Интеграл ∫ C·ds равен

-y , подобно тому как ∫ F·ds=- U ; они отличаются только

масштабом:

U= -∫ F·ds=-m∫ C·ds=my. (14.7)

Зная в каждой точке пространства эту функцию y (х, y , z), можно немедленно вычислить потенциальную энергию тела в любой точке, а именно U ( x , у, z ) — m y (х, у, z ). Теперь, как видите, это стало делом пустяковым. Но на самом деле это от­нюдь не пустяк, потому что иногда намного приятнее описать поле, задав распределение потенциала во всем пространстве, чем задавать С. Вместо трех сложных компонент векторной функции проще задать скалярную функцию y. Кроме того, когда поле создается многими массами, величину y рассчиты­вать легче, чем три компоненты С: потенциалы—скаляры, их можно просто складывать, не заботясь о направлениях сил. А поле С, как мы сейчас увидим, легко восстановить, зная y . Пусть у нас есть точечные массы m 1 , m 2 ,... в точках 1, 2..., и мы хотим знать потенциал y в некоторой произвольной точке Р. Тогда он оказывается простой суммой потенциалов отдельных масс в точке Р:

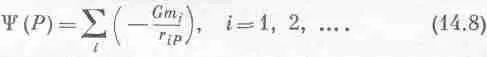
Этой формулой, представляющей потенциал в виде суммы потенциалов отдельных масс, мы пользовались в предыдущей главе, чтобы вычислить потенциал сферического слоя (мы тогда сложили потенциалы всех поясков, на какие был нарезан слой). Итог расчета показан на фиг. 14.4.

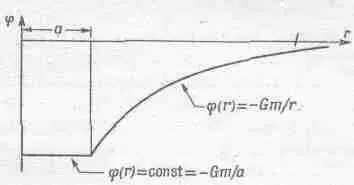
Фиг. 14.4. Потенциал тяготею­щего сферического слоя радиусом а.

Потенциал отрицателен, ра­вен нулю на бесконечности, падает как 1/r, пока r не станет рав­ным а, и затем внутри слоя становится постоянным. Вне слоя потенциал равен — Gm / r (т— масса слоя), что полностью сов­падает с потенциалом точки с массой т, помещенной в центре сферического слоя. Но такое совпадение существует только для точек снаружи слоя, а во внутренних точках потенциал оказывается равным — Gm / a и больше не меняется! А когда потенциал постоянен, то поля нет: если потенциальная энергия не меняется, то сила отсутствует, потому что, когда мы дви­гаем тело из одной внутренней точки в другую, работа, выполняе­мая силой, в точности равна нулю. Почему? Да потому, что ра­бота передвижения тела из одной точки в другую равна минус изменению потенциальной энергии (или соответствующий ин­теграл от поля равен изменению потенциала). Но потенциальная энергия в обеих точках одинакова, значит, ее изменение равно нулю, и поэтому никакой работы при любых движениях внутри сферического слоя не производится. А это возможно лишь тогда, когда внутри слоя нет никаких сил.