Рудольф Рэфф - Эмбрионы, гены и эволюция

Подобно изменениям регуляторных генов, влияющих на сроки или структурную интеграцию, изменения регуляторных генов, контролирующих тканевую дифференцировку, также обладают большим эволюционным потенциалом. Если изменения регуляторных генов двух первых типов вызывают изменения формы органов, то изменения генов этого третьего типа приводят к образованию новых тканей. Одним примером (подробнее см. гл. 12) служит млечная железа, возникновение которой сопровождалось появлением новой ткани, новых белков, новых регуляторных генов и целым набором поведенческих комплексов. Все это сыграло чрезвычайно важную роль в эволюции размножения млекопитающих и заботы о потомстве. Три способа регуляции развития, которые мы здесь бегло рассмотрели, неотделимы друг от друга. Все они участвовали в морфологической эволюции отдельных групп организмов.

Быть может, главная трудность, с которой мы сталкиваемся в нашей попытке понять морфологическую эволюцию в контексте эмбриогенетических механизмов, заключается в том, что формообразование на молекулярном уровне изучено крайне плохо. Дело здесь не только в том, что у нас мало сведений о самих механизмах морфогенеза (перемещения клеток, их взаимодействия, возникновение структурной организации), но и в различных концептуальных подходах к оценке информации, содержащейся в морфологической структуре, и в оценке генетической информации. В качестве иллюстрации этого различия рассмотрим морфогенез не с точки зрения молекулярной генетики, а воспользуемся подходом Д'Арси Томпсона (D'Arcy Thompson), который в своей книге «О росте и форме» (ее первое издание вышло в 1917 г.) впервые применил математику к проблемам формы (рис. 1-1).

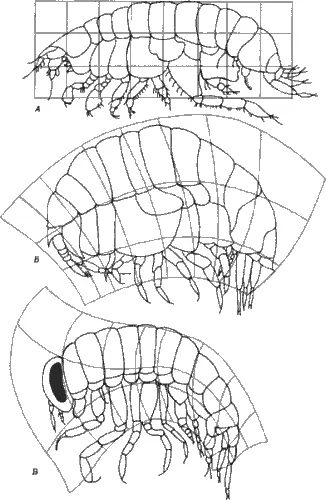
Рис. 1-1.Изменения общей формы тела у некоторых равноногих рачков. А. Вид изображен в прямоугольной системе координат. Б и В . Деформация соответствующих решеток для двух других видов иллюстрирует изменения пропорций в процессе эволюции (Thompson, 1961).

Его цель была проста: « Мы хотим понять, как можно объяснить, по крайней мере в некоторых случаях, форму живых существ и частей живых существ, исходя из физических представлений, и установить, что органических форм, которые противоречили бы физическим и математическим законам, не существует ». Томпсон изложил свою точку зрения в книге, которая изучалась несколькими поколениями биологов, познакомившихся с ее помощью с математическими законами, лежащими в основе формы поверхностей раздела между клетками и строения радиолярий или спирально закрученных раковин и бараньих рогов; с тем, почему скелет позвоночных и мосты построены в соответствии с одними и теми же инженерными законами, и как, используя преобразования декартовых координат, можно изображать эволюционные изменения формы таких сложных объектов, как черепа, рыбы и изоподы (равноногие рачки). Томпсон снял покров непроницаемой тайны с биологической формы и очень изящно показал, что сложные биологические объекты подчиняются физическим и математическим правилам, поддающимся проверке. Однако он уделял мало внимания событиям, происходящим на генетическом или молекулярном уровне (вероятно, это было разумно, потому что эти события и сейчас еще не вполне поняты), а вместо этого сосредоточился на действующих на организм физических силах как непосредственных факторах, определяющих его морфологию.

С изменениями формы, происходящими в период роста, Томпсон справился менее успешно. Математический анализ относительного роста частей организма в течение его развития (аллометрии) был разработан Гексли (Huxley) в начале 30-х годов нашего века. В основном зависимости, наблюдаемые при таком росте, описываются простым уравнением у = bx α, где x и у - размеры двух сравниваемых структур. Аллометрия представляет значительный интерес в смысле понимания эволюционных изменений, однако и в этом случае изменения пропорций организма, сопровождающие рост, не поддаются оценке на генетическом или молекулярном уровне, и, конечно, зависимости здесь значительно сложнее, чем подразумевает простое уравнение аллометрического роста.

Подобным же образом моделирование формы раковин моллюсков на вычислительной машине, произведенное Раупом и Михельсоном (Raup и Michelson), показывает, что для создания объектов с очень изощренной морфологией может оказаться достаточным лишь небольшое число параметров (рис. 1-2). Раковины брюхоногих моллюсков-это сужающиеся к одному концу трубки, закрученные в спираль вокруг неподвижной оси. Для того чтобы создать на машине аналоговую модель настоящих раковин, требуются всего четыре параметра: 1) форма сечения образующей кривой; 2) скорость расширения образующей кривой относительно вращения; 3) расположение и ориентация образующей кривой относительно оси; 4) скорость движения образующей кривой вниз по оси. Эти простые параметры описывают форму создаваемого объекта, но они не имеют отношения к генетической программе или к тем действительным механизмам, при помощи которых организмы реализуют генетическую программу морфогенеза.