Джонс Морган - Решение проблем по методикам спецслужб. 14 мощных инструментов

В случае с задачей «Совещание по планированию» каждая матрица должна содержать три варианта (Нью-Йорк, Флорида и Вермонт). Так как при принятии подобных решений решающее значение часто имеет погода – ведь именно от погоды зависит, получат ли участники удовольствие от запланированного отдыха, – то рассматриваемые нами возможные последствия будут связаны именно с этим фактором: рассмотрим «тепло и солнечно» и «холодно и дождливо». Постройте три матрицы анализа полезности для каждой из рассматриваемых точек зрения. Не включайте в таблицу колонку «Рейтинг» (я объясню причины чуть ниже).

В табл. 16.1 показаны все три матрицы.

Таблица 16.1

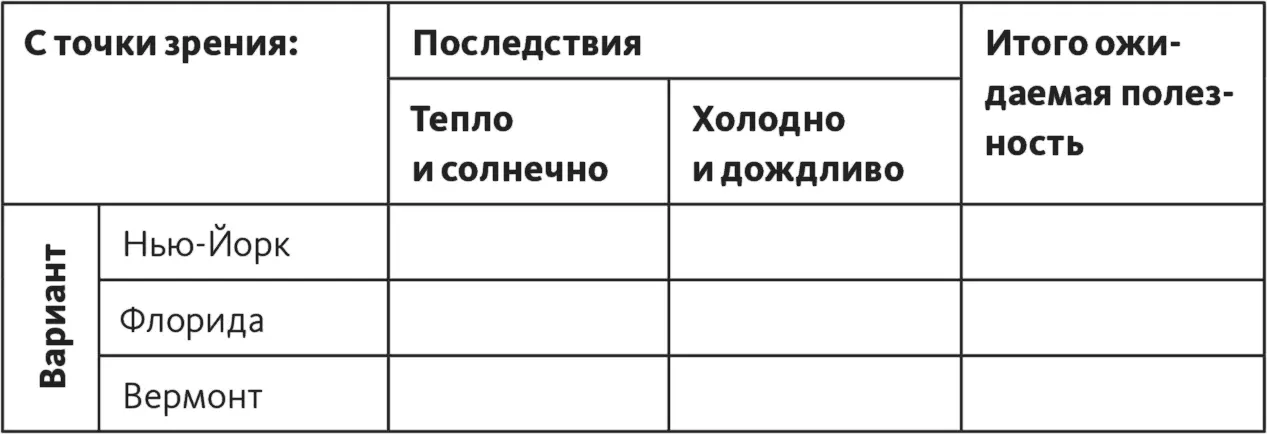
Процесс анализа полезности при работе с разными точками зрения используется тот же, что мы применяли в предыдущих главах: нужно задать вопрос для определения полезности каждой из комбинаций «вариант – полезность», оценить полезность, затем задать вопрос для определения вероятности наступления последствий, оценить вероятности, подсчитать ожидаемую полезность, сложить показатели ожидаемой полезности для каждого из вариантов, записать результат в колонку «Итого ожидаемая полезность».

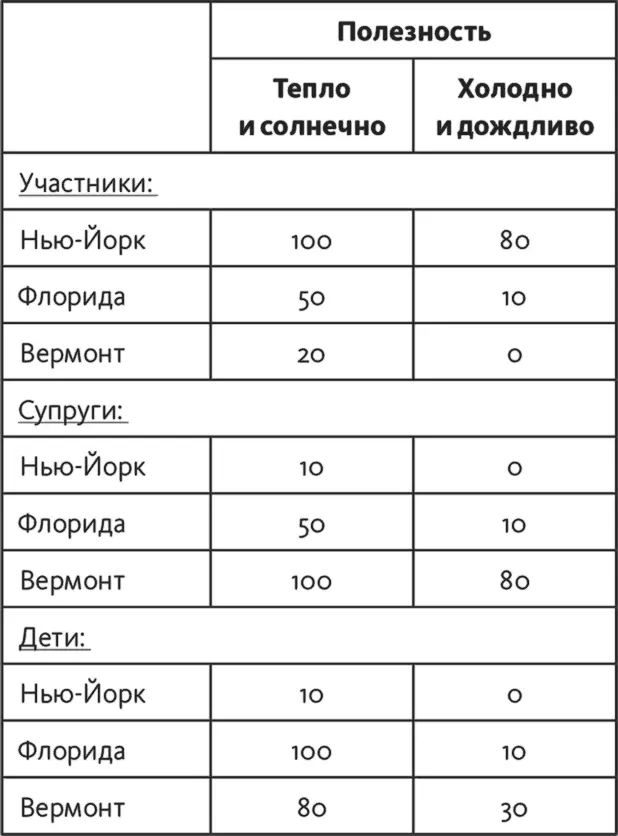
Для ускорения работы я проставил показатели полезности для всех трех матриц (табл. 16.2). Эти величины я получил, задав вопрос о полезности каждой из комбинаций «вариант – полезность», к примеру: «Если совещание будет проводиться в Нью-Йорке и погода будет теплой и солнечной, какова полезность этого варианта с точки зрения удовольствия участников от мероприятия?» Внесите показатели полезности в свои матрицы.

Таблица 16.2

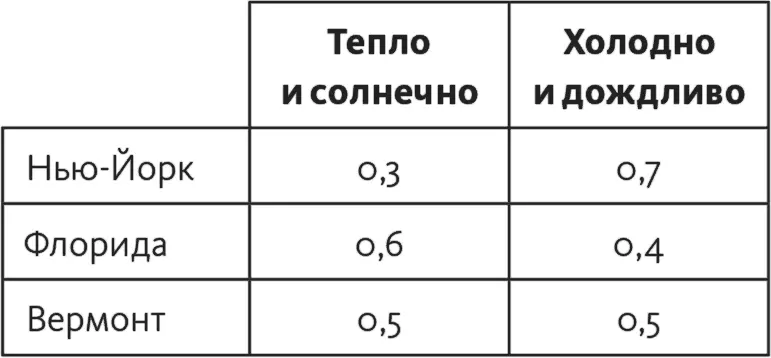
В табл. 16.3 приводится прогноз погоды с указанием вероятности каждого из возможных вариантов. Внесите вероятности в матрицы, рассчитайте ожидаемую полезность, потом сложите полученные цифры для каждого варианта и внесите суммы в колонку «Итого ожидаемая полезность».

Таблица 16.3

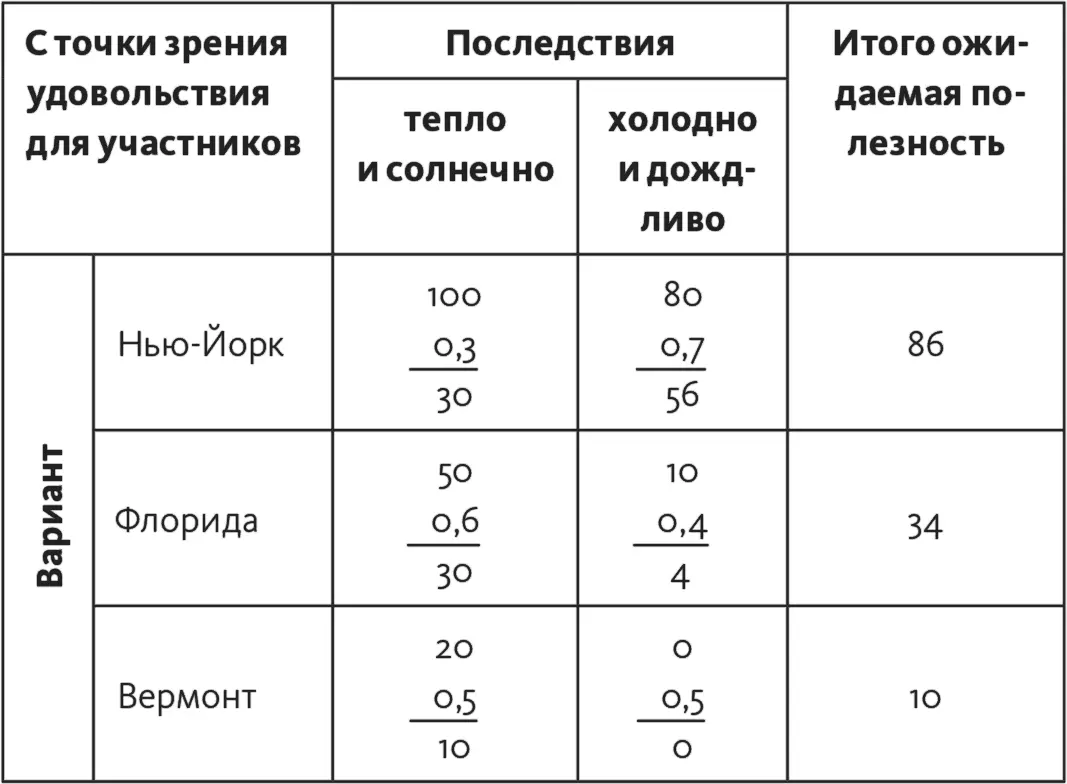
В табл. 16.4 показаны расчеты для каждой из матриц.

Таблица 16.4

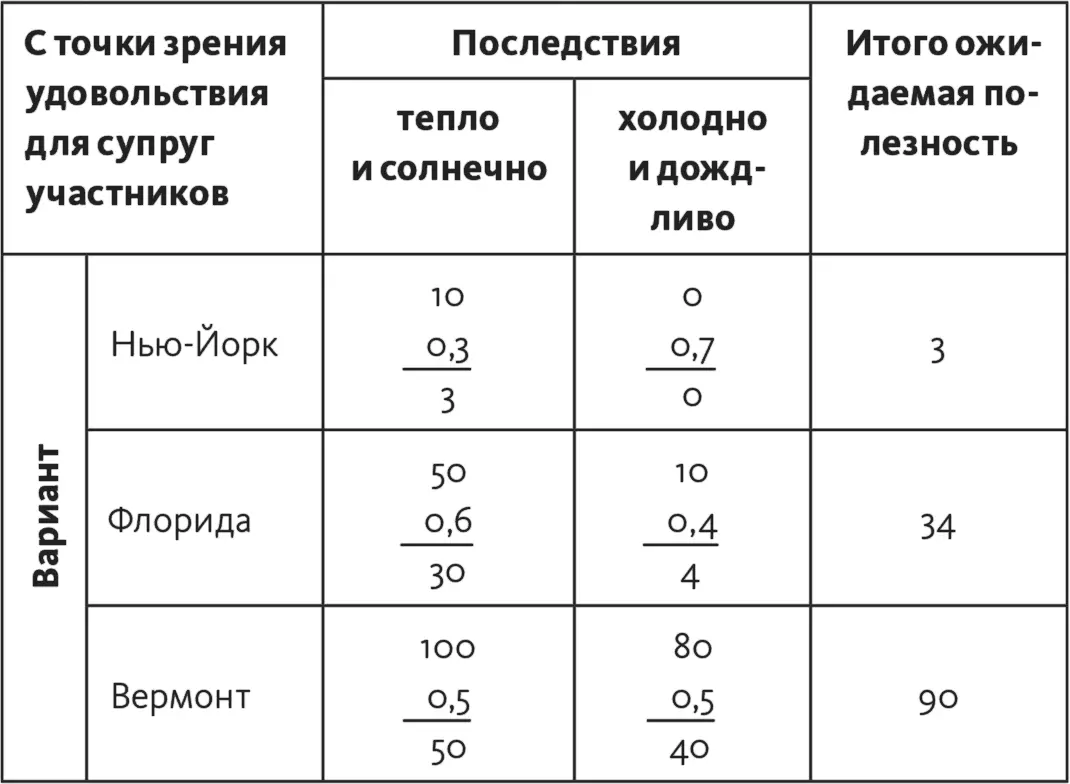
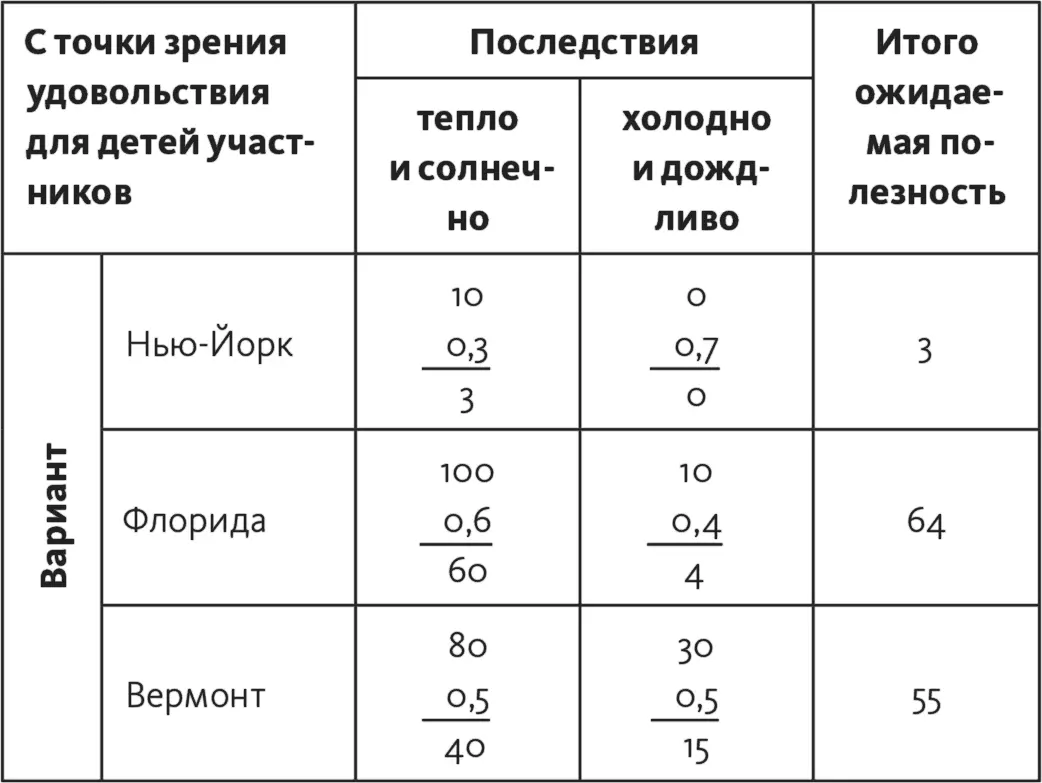
Следующий шаг: нужно объединить все варианты и построить рейтинг. Для этого мы перенесем показатели ожидаемой полезности каждого из вариантов из трех матриц в четвертую, объединенную матрицу (табл. 16.5). Постройте у себя такую же объединенную матрицу и внесите в нее величины ожидаемой полезности из матриц, построенных для каждой из рассматриваемых точек зрения.

Таблица 16.5

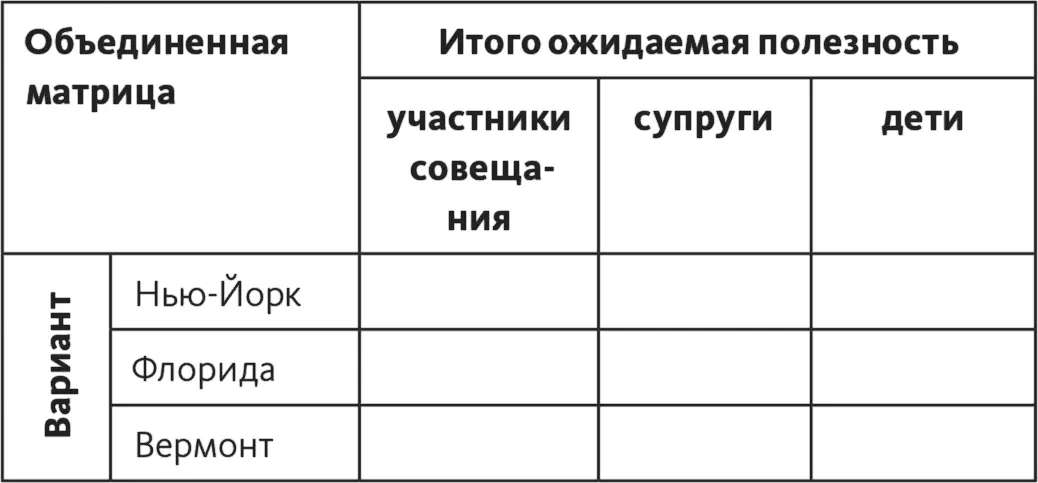
Объединенная матрица приводится в табл. 16.6.

Таблица 16.6

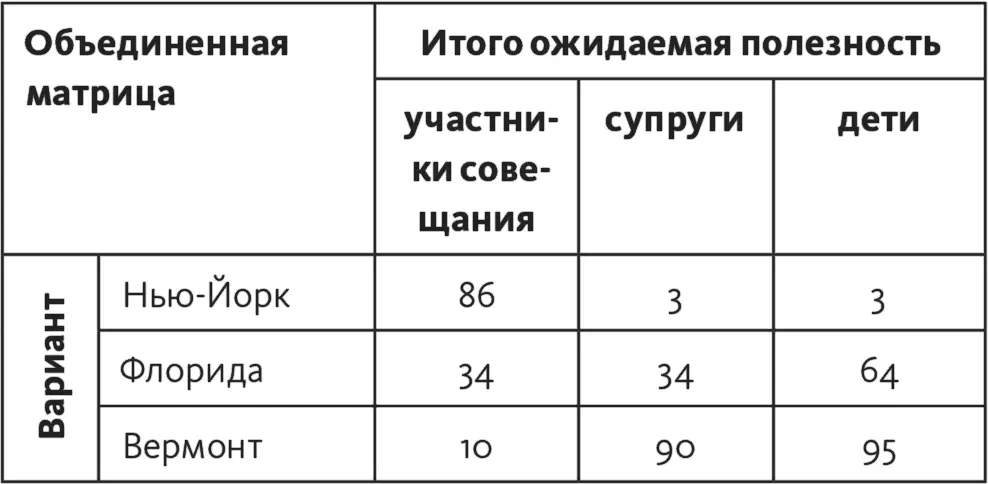
Разумеется, мы можем просто сложить величины ожидаемой полезности для каждого варианта и согласиться, что наиболее предпочтителен тот, что наберет наибольший результат. Но это возможно, только если административная команда действует по принципу Лапласа: если у них нет оснований считать одну из трех точек зрения более существенной, чем прочие, то есть если все три точки зрения равноценны.

Но что если для тех, кто разрабатывает программу и выбирает место ее проведения, удовольствие от программы самих участников гораздо важнее, чем удовольствие их супруг и детей? Тогда можно всем трем точкам зрения назначить относительный вес, скажем, 0,8 для участников, 0,1 для супруг и 0,1 для детей. Впишите эти коэффициенты в названия колонок, относящихся к рассматриваемой группе, и добавьте еще две колонки, «Итого взвешенная ожидаемая полезность» и «Рейтинг». Теперь перемножьте величины ожидаемой полезности на соответствующий вес, запишите результат в колонку «Итого взвешенная ожидаемая полезность», затем отразите место каждого из вариантов в колонке «Рейтинг».