Джонс Морган - Решение проблем по методикам спецслужб. 14 мощных инструментов

Провести анализ полезности не так уж сложно – важно только соблюдать ключевые принципы. Некоторым поначалу кажется, что это просто еще одна арифметическая задачка, в силу чего они начинают сомневаться в достоверности и ценности полученных результатов. Их беспокоит, что если требуются всего лишь простые расчеты, то разум и интеллект вроде бы оказываются не вовлеченными в работу. Но на самом деле беспокойство вызывает тот факт, что этот аналитический инструмент оказывается им совершенно незнаком. Я и сам о нем узнал всего лишь 14 лет назад и с тех пор научился им уверенно пользоваться, ведь процесс мне стал полностью понятен, а результат кажется вполне надежным.

Примечания к Главе 14

Для оценки полезности матрица-таблица заметно удобнее дерева, и тому есть две причины. Во-первых, относительную разницу в степени полезности возможных последствий проще анализировать в формате матрицы. Во-вторых, в таблице проще производить необходимые расчеты. Отчасти дело тут и в том, что эти два инструмента организованы по-разному: дерево оказывается слишком перегружено информацией, оно расползается, иногда оказывается несимметричным, а матрица остается компактной, ясно структурированной, симметричной. Кроме того, в матрице все внимание уделяется исключительно альтернативным вариантам последствий, в то время как в рамках дерева мы вначале представляем все возможные сценарии, а уже потом соответствующие последствия. Работа над сценариями неизбежно отвлекает наше внимание от анализа возможных последствий.

Так чем лучше пользоваться для анализа полезности – матрицей или деревом? Очевидно, что ответ зависит от сути проблемы и предпочтений самого аналитика, работающего над проблемой. Какой бы инструмент мы ни выбрали, основные шаги остаются теми же: нужно построить структуру, то есть матрицу или дерево, записать все варианты сценариев и возможные последствия, решить, с чьей точки зрения будет вестись анализ вариантов, оценить полезности и вероятности, произвести расчет ожидаемых величин и сформировать рейтинг.

С помощью матрицы делать необходимые расчеты проще, поэтому она лучше подходит для работы над проблемами, где требуется посмотреть на ситуацию с разных углов и сравнить возможные последствия разных типов. Я подробно расскажу о подходах к решению подобных задач в следующих двух главах.

А сейчас позвольте мне показать, как использовать матрицу полезности. В табл. 15.1 показаны основные элементы матрицы полезности.

Таблица 15.1. Матрица полезности

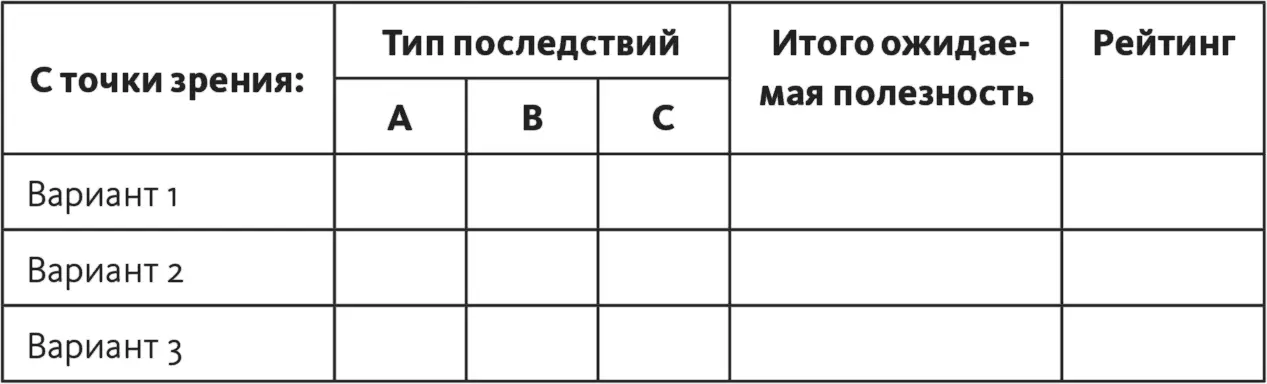
В верхнем левом углу мы записываем, с чьей точки зрения ведется анализ. В левой колонке перечисляем все рассматриваемые варианты. Класс рассматриваемых последствий указываем в ячейке над колонками, в названиях которых записываем сами варианты последствий. Для каждой комбинации «вариант – последствия» в матрице должна быть отдельная ячейка, в которой мы записываем полезность и вероятность наступления этой комбинации, а также рассчитанную ожидаемую полезность. Затем суммируем показатели ожидаемой полезности для каждого варианта, результат записываем в колонке «Итого ожидаемая полезность». В последней колонке проставляем позиции в рейтинге.

Сейчас я построю матрицу на основе трех деревьев (рис. 15.1), которые мы делали для упражнения 39, «Товары из Японии», и вам все станет понятнее. Итоговая матрица приводится в табл. 15.2.

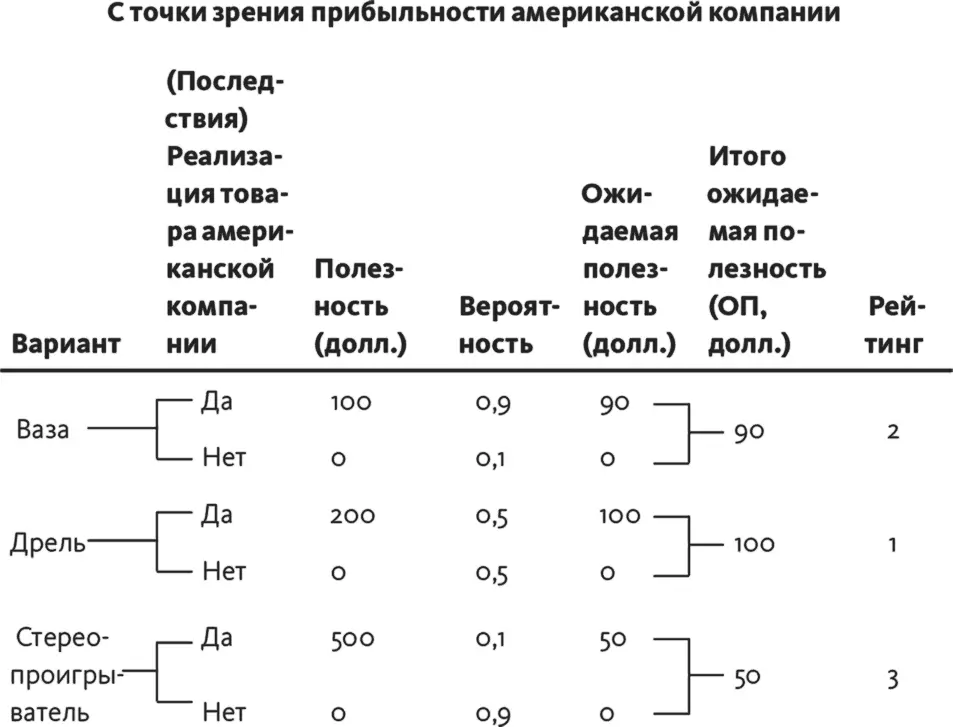
Рис. 15.1

Таблица 15.2

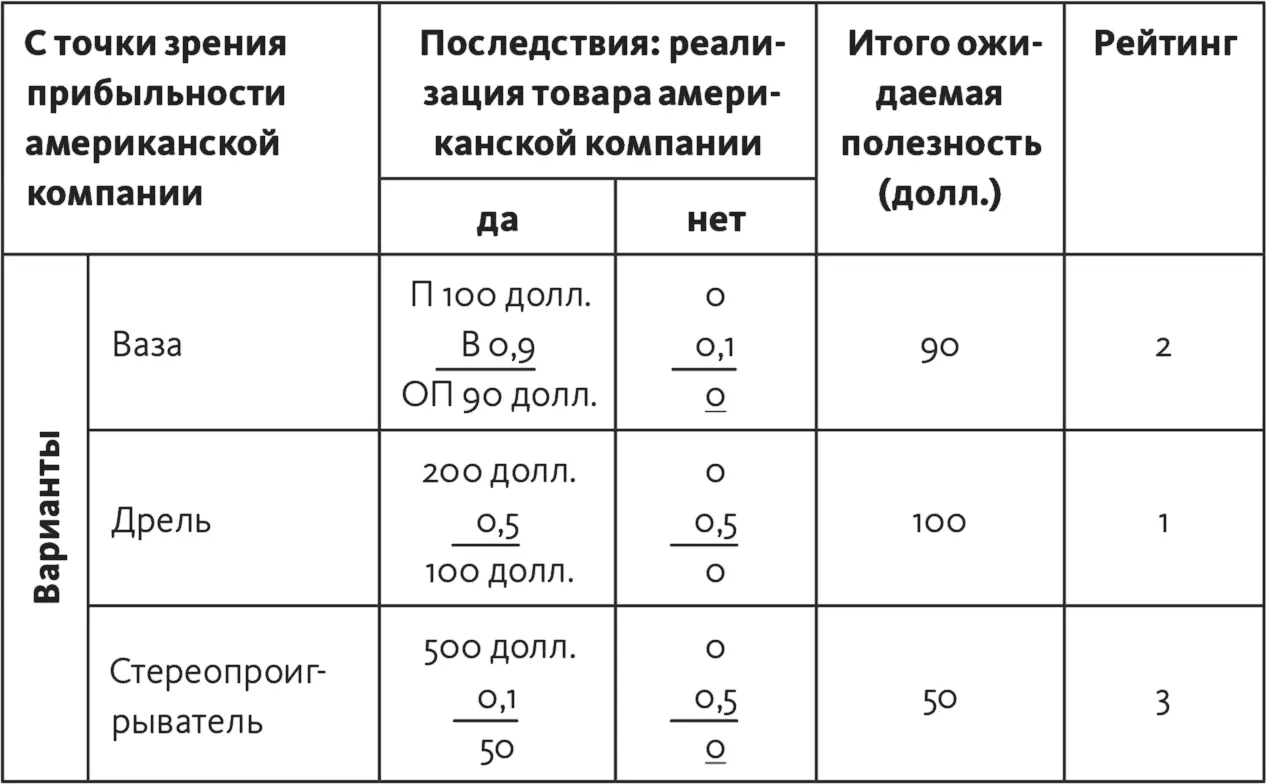
Обратите внимание, как матрица действительно помогает сфокусироваться именно на возможных последствиях: все цифры для каждой комбинации «вариант – последствия» аккуратно заносятся в одну ячейку. Мне лично гораздо проще замечать закономерности, различия и сходства, когда я работаю с матрицей, а не с деревом, – но вообще это вопрос личных предпочтений и привычек, конечно.

Чтобы лучше понять, как работать с матрицей полезности, потренируйтесь и преобразуйте деревья (рис. 15.2), которые мы с вами строили для упражнения «Куры-несушки»из главы 14.

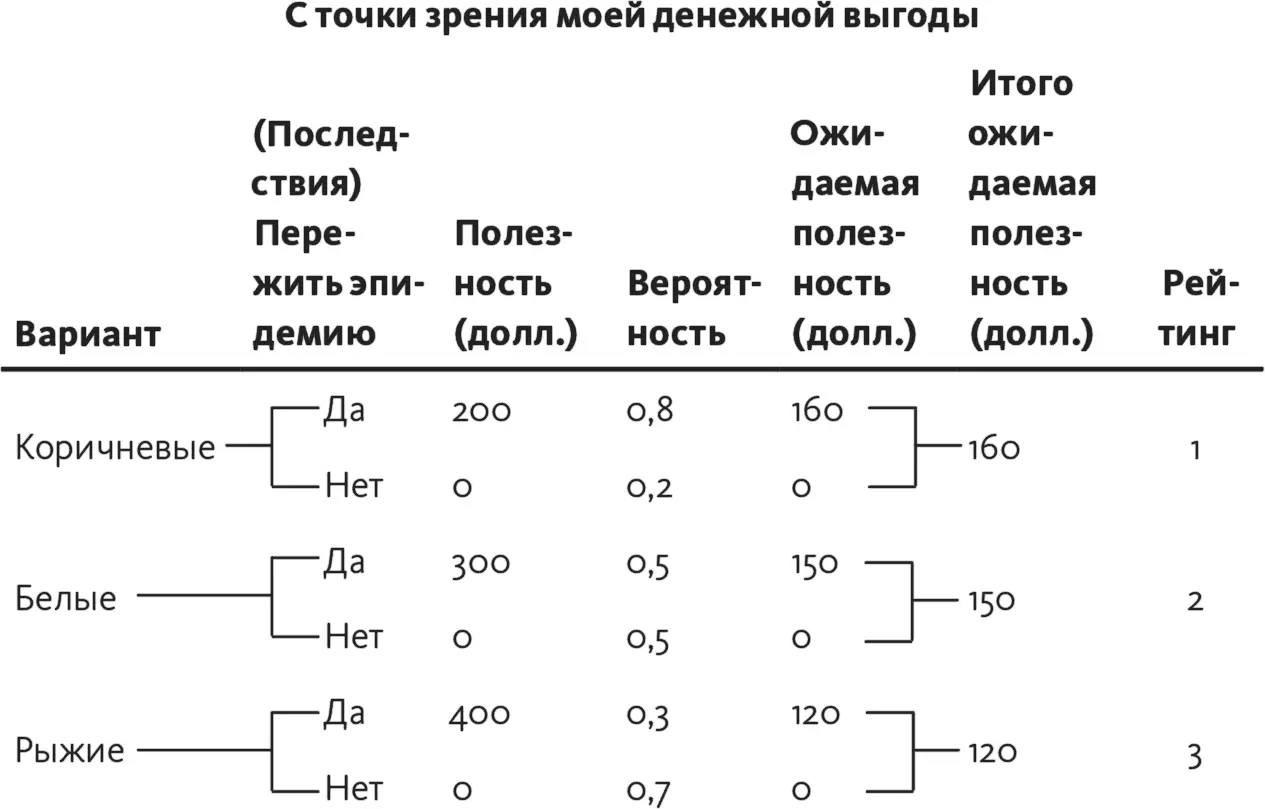
Рис. 15.2