Али Альмоссави - Хакни рутину. Как алгоритмы помогают справляться с беспорядком, не тупить в супермаркете и жить проще

Прежде чем читать дальше, проработайте эти варианты, используя ручку и бумагу или любой другой реквизит. Подумайте о том, какую цель преследует каждый отдельный шаг на примере сцен, перечисленных ниже.

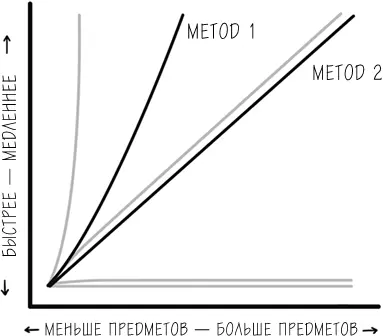
Если в куче всего четыре носка, то неважно, какой метод будет использовать Марджи: она быстро справится с задачей. А теперь представьте, что перед ней лежит сотня носков. Если она выберет первый метод, то с большой вероятностью будет снова и снова натыкаться на один и тот же носок, поскольку он остается в общей куче. Вытащив его в первый раз, она не извлечет из него никакой информации.

При использовании второго метода перед ней вырастет шеренга носков без пары, и, следовательно, она будет брать каждый носок из кучи вещей всего один раз. Второй метод оказывается быстрее, потому что он опирается на память – точнее говоря, на то, что мы иногда называем справочными таблицами, или сверхоперативной памятью.

Полезно представить справочную таблицу как сборник уникальных идентификаторов – клавиш, каждая из которых указывает на какую-либо связанную с ней информацию. Вы в буквальном смысле видите надписи на клавишах. Мы называем этот тип представления парой «ключ—значение» .

В случае с носками наши клавиши скорее всего будут цветными. Когда Марджи находит красный носок, она ищет тот же цвет среди непарных. Найдя его, она может вводить дополнительные идентификаторы/признаки, например стиль или оттенок. Если пара так и не найдена, она создает новую область под названием «красное» с единственным красным носком в ней.

Как эти два метода соотносятся друг с другом? [10] Есть более сложные методы изучения скорости роста. Один из них – узнать, не растет ли определенный метод быстрее, чем показанная скорость (известная под названием большое-о), или медленнее, чем показанная скорость (известная как большое-Ώ, т. е. «большая омега»). Другой метод – посмотреть, описывают ли скорости роста лучшие, худшие или средние случаи. Мы поговорим обо всех этих случаях позже ( прим. автора ). Мы уже заметили, что работа по методу 1 сильно замедляется по сравнению с методом 2 по мере увеличения носков в куче. На самом деле существует гораздо больше способов решения задачи. Но нам сейчас важно показать, чем именно эти два метода радикально отличаются друг от друга, не упоминая другие, чья эффективность может находиться где-то посередине. К примеру, Марджи могла бы применить принцип Дирихле – то есть вытаскивать по шесть носков из кучи одновременно и подбирать пары таким способом.

Вытаскивая носок из кучи, мы достаточно быстро сможем подобрать ему пару. Кратковременная память большинства людей прекрасно работает с группами, насчитывающими плюс-минус десять предметов, а именно такими величинами мы оперируем в данный момент. Натыкаясь на носок, который мы уже откладывали в сторону, мы должны воскликнуть: «А, да – я его уже видел!» Если вы когда-нибудь играли в карточную игру «Память», преимущества и недостатки этой системы должны быть вам хорошо знакомы.

Если бы у нас было гораздо больше носков разных типов и цветов, то ряд непарных оказался бы таким длинным, что нам пришлось бы заново пересматривать всю их последовательность каждый раз, когда мы вытаскиваем из кучи новый. Это трудоемко и долго, особенно если искомый предмет оказывается в самом конце.

В 1953 году математик Ханс Питер Лун, работавший в корпорации «IBM», выдвинул идею, которая положила начало созданию альтернативной структуры, облегчающей потенциальную замедленность, присущую любому комплексному поиску. Эта структура иногда называется ассоциативным массивом, или хеш-таблицей (посыплем еще немного соли на раны старушки Марджи). Хеш-таблица делает то же, что и массив: она сохраняет вещи в коллекции, но использует более строгую последовательность (например, большой черный носок всегда идет после красного носка) для немедленного так называемого поиска за постоянное время . [11] В этом примере Марджи не особенно заботится о том, в каком порядке лежат неразобранные носки. Все, что ее беспокоит, – все носки должны быть отложены в одну сторону.

Он называется непрерывным, потому что не зависит от длины последовательности. Впрочем, это не всегда так. Многие вещи в программном обеспечении, к неудовольствию исследователей и практиков, не подчиняются фундаментальным законам – в отличие от природы. Но здесь мы допускаем, что из-за малого числа несопоставимых носков синапсы Марджи будут возбуждаться быстро и вызывать почти немедленную реакцию.