Джон Ди - Иероглифическая монада

Те, кто могут увести нас из Сада Гесперид, и заставить заглянуть прямо в зеркало, скажут, что это утверждение выведено не из чего иного, как только из нашей Монады.

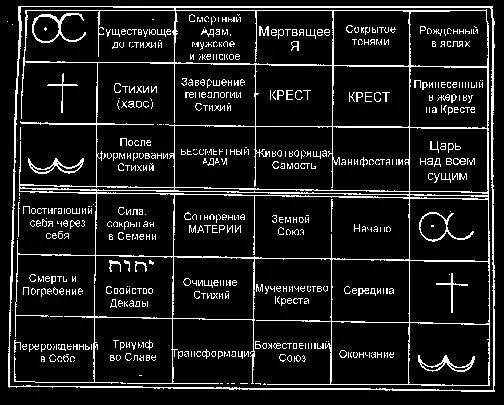
Но прямая линия, каковая проявляется в нашей Альфе, гомологична той, которая, отделившись в ходе анализа нашего Креста, определяется буквой М. Таким же путем можно выяснить, откуда происходит всё остальное. В связи с этим рассмотрите следующий рисунок:

Мне известно, что в этих нескольких словах я дал не только основные принципы, но также и способ, как защитить энергию огня и небесный источник для тех, кто способен увидеть это, так что они смогут истово вслушаться в слова великого Демокрита, и не усомниться в том, что это не мифическая догма, но тайна и мистерия, в соответствии с которой готовится лекарство души, освобождающее от всех страданий, и доступное тем, кто возжелал его и был научен; его ищут в Гласе Создателя Вселенной, и люди, вдохновленные Господом и рожденные заново, смогут познать его посредством совершенного учения языков мистики.

Теперь мы представим в виде диаграммы те пропорции, которые уже были рассмотрены нами в иероглифической конструкции нашей Монады, и каковые следует рассмотреть всякому, кто хотел бы выгравировать их на своих печатях или кольцах, или же использовать каким-либо другим образом. Во имя Иисуса Христа, распятого на Кресте, я провозглашаю, что Дух пишет это через меня; я также надеюсь и верю, что являюсь простым писчим пером, оставляющим знаки на бумаге. Дух ведет нас к нашему Кресту Стихий, вместе со всеми представляемыми им соотношениями, к которым можно придти в ходе рассуждений на тему рассматриваемого нами предмета. Все, существующее под Лунным небом, содержит в себе принцип собственного существования, и образовано путем коагуляции четырех Стихий, так как в противном случае оно само являлось бы первичной субстанцией, и так же нет ничего в сотворенном мире, образованного Стихиями в равной пропорции или равной силой, о чем, кстати, не догадываются невежды. Посредством нашего Искусства, они [Стихии] могут быть приведены к равенству в определенном аспекте, что хорошо известно мудрым; таким образом, части нашего Креста мы делаем и равными, и неравными.

С другой стороны, мы в этом случае можем провозгласить как подобие, так и различие, как единство, так и множественность, подтверждая скрытые свойства равностороннего Креста, как уже говорилось ранее.

Если бы мы изложили все известные нам толкования устанавливаемых таким образом пропорций, или применили другой способ их демонстрации, который еще не был использован, хотя для Мудрых и так уже было сказано достаточно, мы преступили бы рамки допустимой ясности, небезосновательно установленные для данного изложения.

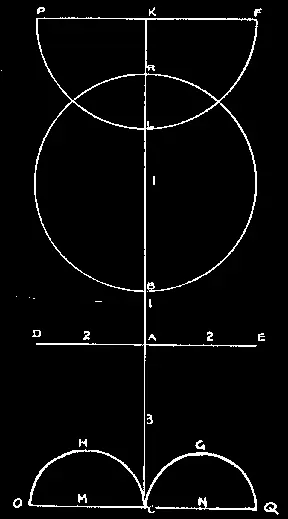
Возьмем любую точку, например А, и проведем прямую линию через нее, получив САК. Разделим теперь линию СК в точке А при помощи другой линии под прямым углом, и назовем ее DAE. Теперь выберем точку в любом месте на участке АК, — скажем, В, — и получим таким образом единичную меру АВ, каковая станет общей для всей нашей работы. Отмерим эту величину АВ трижды, считая от А, и получим отрезок АС. Теперь возьмем два АВ и отложим отрезки в обе стороны от А на линии DAE, получив отрезок DE, равный четырем АВ. Так мы составили наш Крест четырех Стихий, или, говоря другими словами, Кватернер, образованный линиями АВ, АС, AD, АЕ. Теперь на линии ВК отложим расстояние, равное AD, и отметим точку I. Взяв ее за центр, радиусом IB опишем круг, пересекающий АК в точке R: от R в направлении К отмерим расстояние, равное АВ, и назовем его отрезком RK. Через точку К проведем линию под прямым углом к центральной линии, образовав перпендикулярную линию PКF. От точки К отметим в направлении F расстояние, равное AD, которое образует отрезок КF; теперь из центра К радиусом КF опишем полукруг FLP, в котором FKP — диаметр. Наконец, через точку С под прямым углом проведем линию достаточной длины и назовем ее OCQ. На участке СО отмерим от точки С отрезок длиной АВ и поставим точку М, после чего взяв ее за центр проведем полукруг СНО радиусом МС. Таким же образом на участке CQ отмерим отрезок длиной АВ и назовем его CN, и из центра N радиусом CN проведем полукруг CGQ, у которого диаметром является CNQ. Теперь мы можем утверждать, что все необходимые соотношения нашей Монады описаны и разъяснены.