Вильгельм Оствальд - Искусство цвета. Цветоведение - теория цветового пространства

Если мы на стороне WS однотонного треугольника расположим ахроматические цвета так, чтобы отрезки между ступенями были пропорциональны содержанию белого цвета, как того требует изображение однотонного треугольника, то мы получим, согласно изложенному выше, неправильную шкалу серых цветов, растянутую в светлой части и слишком стиснутую в темной. То же самое мы замечаем на обеих других сторонах треугольника, на VW и VS. Вдоль линии VW расположены, начиная от W, на довольно далеком расстоянии друг от друга бледные цвета, у которых еле заметен их тон. Ближе к V мы видам более насыщенные цвета, которые очень притиснуты друг к другу. Что же касается цветов, расположенных по линии VS то начиная с точки V цвет сначала совсем: не меняется. Только во второй половине появляется черный цвет, и у точки S темные цвета уже близко расположены друг около друга.

Для стороны WS нам причина вышеописанного хорошо известна. Она находит свое объяснение в законе Фехнера, который гласит, содержание белого цвета должно представлять собою нисходящий геометрический ряд для того, чтобы светлота серых цветов равномерно уменьшалась согласно арифметическому ряду.

То же мы видим и у двух других сторон. Это доказывает, что закон Фехнера применим также и в отношении смесей полного цвета с белым или черным. В ряду: белый – полный цвет, роль черного цвета принимает на себя этот последний, так как белый цвет ее выполнять не может. В ряду же полный цвет – черный, полный цвет должен взять на себя роль белого цвета, так как черный не может влиять как белый.

Открытие и этих двух законов стало тогда только возможным, когда стало доступным измерение цветов. Таким образом, на каждом шагу нам встречаются такие открытия, которые были совершенно недоступны качественному периоду учения о цветах.

Если, согласно закону Фехнера, мы разделим стороны однотонного треугольника, который нами выше описан так, чтобы цвета казались нам одинаково отстоящими друг от друга, то мы получим расположенно изображаемое рис. 13.

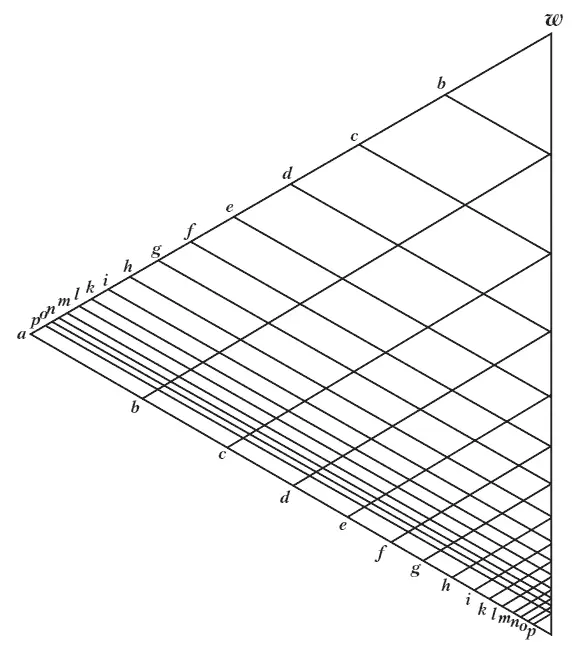
Рис. 13

Тут возникает, однако, потребность расположить цвета в треугольнике таким образом, чтобы одинаковым расстояниям в пространстве соответствовали бы одинаковые и психологически расстояния. Для этого необходимо треугольник так растянуть (в нижней его части) вниз, чтобы отрезки (расстояния) bc, cd, de и т. д. выравнялись бы. Так как это логарифмическое деление теоретически ведет в бесконечность, то вся сторона VS со своими конечными точками V и S удаляется в бесконечность. Практически же этого не случается, так как мы совершенно не в состоянии приготовить ни краски чистых цветов, в которых отсутствовал бы белый цвет, ни краски черных цветов, в которых отсутствовал бы белый.

Мы называем описанный выше (рис. 8–12) треугольник аналитическим, так как он представляет собою непосредственный результат анализа цветов. Новый же треугольник, расположенный согласно закону Фехнера, мы называем логарифмическим, или же треугольником Фехнера. В практике мы будем пользоваться почти исключительно треугольником Фехнера, так как и для норм и для гармонии необходимы психологически равные расстояния между ступенями.

Важно иметь представление о том, какие изменения вызывает вышеописанное растяжение треугольника. Сразу можно заметить, что в треугольнике (рис. 13) равно-белые как и равно-черные цвета сохраняют свое положение. Они только растягиваются на одинаковые расстояния параллельно их первоначальному положению.

Иначе дело обстоит с равно-чистыми цветами. Если мы проведем соответствующие линии параллельно WS, то такие линии не будут соединять точек пересечения линий цветов равно-белых или равно-черных, как это имело место в аналитическом треугольнике, а пойдут беспорядочно через косоугольники, составленные линиями тех и других. Если же соединим соответственные точки пересечения этих линий (углы ромбов), то получим ряд линий, которые в аналитическом треугольнике сходятся к углу S.

При превращении аналитического треугольника в логарифмический, отрезки равно-белых и равно-черных цветов становятся одинаковыми, а соответственные угловые точки ромбов находятся на прямых линиях, параллельных WS. Это и должно быть, раз точка S удаляется в бесконечность, а линии, стремящиеся к бесконечно удаленной точке, параллельны между собой.