Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]

Как это можно применить в бизнесе? «Серийные номера» (то есть последовательные серии) можно найти в современном мире где угодно. Так, компании бесплатно предоставляют конкурентам информацию о своем объеме производства, просто указывая на товарах серийные номера, которые может увидеть любой покупатель. (Однако, чтобы быть случайной, такая выборочная совокупность должна состоять из товаров, купленных в разных магазинах.) Аналогичным образом несколько страниц из выброшенного отчета конкурента или цифр из квитанции могут многое рассказать об остальных страницах отчета или обо всех квитанциях за данный день. Я вовсе не призываю вас копаться в отбросах, но исследование содержимого мусорных контейнеров нередко позволяет решить интересные задачи по измерению.

Обычно мы хотим что-то измерить, так как требуется обосновать какое-то решение. И для всех решений обычно имеется некое пороговое значение: если интересующий нас показатель окажется выше его, то мы примем одно решение, а если ниже, то другое. Но статистические методы в большинстве своем не занимаются выяснением, при каком значении X следует принять то или иное решение. Я хочу познакомить вас с таким статистическим методом, который позволяет не только снизить неопределенность в целом, но и сравнить интересующий показатель с важным пороговым значением.

Предположим, требуется определить средние затраты времени сотрудников на совещания, которые в наш век Интернета могли бы проводиться и дистанционно. Работники не теряли бы время на дорогу, а совещания не срывались бы из-за проблем с транспортом. Чтобы решить, следует ли проводить данное совещание дистанционно, нужно выяснить, что на нем происходит. Если сотрудники, которые и так постоянно общаются друг с другом, обсуждают рутинные вопросы, но ради этого кому-то приходится ехать издалека, то подобное мероприятие, наверное, лучше проводить дистанционно. Начнем с калиброванной оценки времени, необходимого среднему сотруднику на то, чтобы попасть на совещание, которое могло бы проводиться дистанционно (3–15 %). Далее определяем, что если этот показатель превысит 7 %, то инвестировать немалые средства в подобные виртуальные мероприятия стоит. Расчет ожидаемой стоимости полной информации показывает, что необходимо израсходовать не больше 15 000 дол. на исследования по этому вопросу. Согласно нашему правилу определения затрат на проведение измерений, можно потратить на эти цели примерно 1500 дол., так что если в компании тысячи сотрудников, то сплошной опрос всех участников совещаний абсолютно исключен.

Предположим, что мы выбрали 10 человек и после подробного анализа времени, которое они тратят на дорогу и проводившиеся в последнее время совещания, выяснилось, что только один сотрудник расходует менее 7 % своего времени на эти виды деятельности. Какова, с учетом этой информации, вероятность того, что интересующий нас средний показатель действительно меньше 7 % и подобные инвестиции совершенно неоправданны? Ответ на уровне здравого смысла — один к десяти, или 10 %. Но это как раз тот случай, когда здравый смысл совсем не так полезен, как немного математики. На самом деле эта вероятность намного меньше.

Рисунок 9.4 показывает, как можно оценить вероятность того, что медиана генеральной совокупности находится по одну сторону порога при условии, что половина или большинство значений малой выборки — по другую сторону.

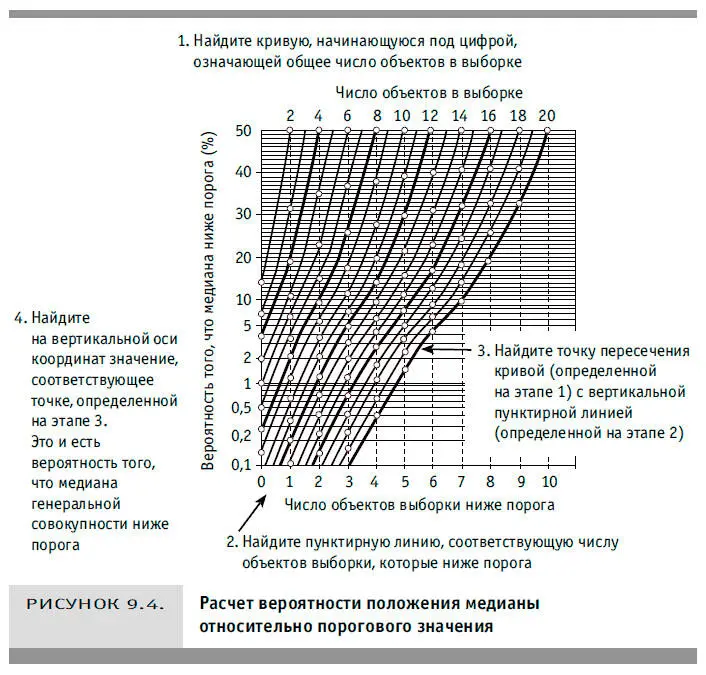
Попрактикуйтесь в обращении с рисунком 9.4.

1. Найдите в верхней части диаграммы, где указаны размеры выборок, цифру 10. Проследите, куда ведет сплошная кривая, соединяющая эту цифру с вертикальной осью координат.

2. Найдите в нижней части рисунка, где указано число объектов выборки ниже порогового, цифру 1. Проследите, куда ведет соответствующая этой цифре вертикальная пунктирная линия.

3. Найдите точку пересечения кривой и пунктирной линий.

4. Соответствующий этой точке процентный показатель на вертикальной оси координат (0,6 %) показывает вероятность того, что медиана такой выборки меньше порогового значения.

Данная малая выборка сигнализирует: вероятность того, что среднее значение совокупности окажется ниже порога, заметно меньше 1 %. Хоть эта статистика и кажется контринтуитивной [26] Нестереотипной. — Примеч. редактора. , но факт остается фактом: неопределенность положения медианы (или даже среднего значения) генеральной совокупности относительно порога можно снизить очень быстро. Предположим, что мы отобрали из генеральной совокупности всего четыре объекта и ни один из них не оказался ниже порогового. Обратившись снова к рисунку 9.4, мы обнаружим, что вероятность нахождения медианы ниже порога составляет чуть менее 4 %, а вероятность ее положения выше него — соответственно 96 %. То, что выборочная совокупность всего из четырех объектов настолько снижает неопределенность, может показаться удивительным, но несложные расчеты или моделирование методом Монте-Карло это подтверждают.