Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]

Если вы проводите важные измерения с высокой стоимостью информации, возможно, стоит проделать описанные мною дополнительные расчеты и разбить распределение на большое число мелких фрагментов. Но чтобы не составлять такую таблицу с нуля, скачайте таблицы «Анализа стоимости информации» и примеры со вспомогательного веб-сайта www.howtomeasureanything.com

В последнем примере с ожидаемой стоимостью полной информации мы оценили затраты на полное устранение неопределенности, а не ее снижение. Расчет EVPI полезен сам по себе, поскольку, по крайней мере, позволяет узнать потолок стоимости информации, который не должен быть превышен при осуществлении измерений. Однако нередко приходится довольствоваться простым снижением неопределенности, особенно когда речь идет о прогнозе, например, роста продаж в результате проведения рекламных кампаний. В таких случаях полезно знать не только максимальную сумму, которую можно израсходовать в идеальных условиях, но и во что обойдется измерение в реальной жизни (обязательно сопровождаемое реальной погрешностью). Иными словами, нам надо знать ожидаемую стоимость информации, а не ожидаемую стоимость полной информации.

Ожидаемую стоимость информации также лучше всего рассчитывать с помощью более сложного моделирования, но мы можем сделать несколько простых оценок. Для этого полезно мысленно представить себе, как выглядит график зависимости EVI от объема информации (см. рис. 7.3).

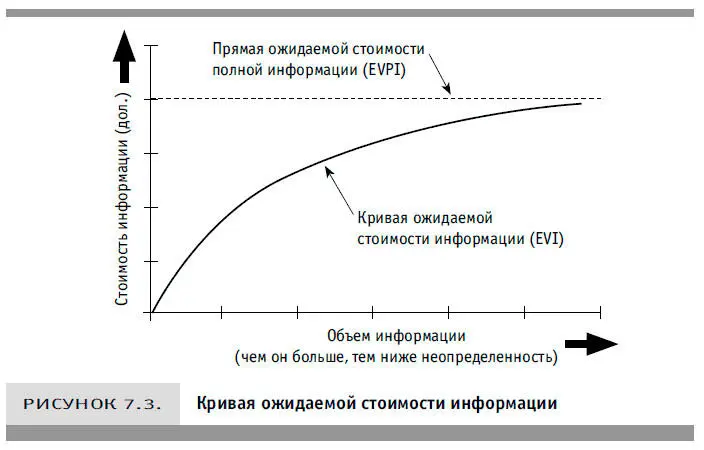
Кривая EVI обычно имеет выпуклый вид и асимптотический характер. Значит, стоимость информации сначала стремится к быстрому росту с каждым небольшим снижением неопределенности, а затем, когда неопределенность приближается к нулю, стабилизируется. Как видно из рисунка, стоимость информации растет очень быстро, выходя на асимптоту на уровне EVPI (которую, конечно, никогда не превышает).

Необходимо также иметь в виду, что график EVI для нормального распределения обычно ближе к прямой, чем тот же график для бинарного или равномерного распределений. При нормальном распределении ожидаемая стоимость информации, снижающей неопределенность первоначального интервала значений вдвое, равна половине EVPI; информации, снижающей неопределенность в четыре раза, — одной четвертой EVPI и т. д. Кривая EVI для нормального распределения, конечно, не имеет вида прямой, поскольку должна приближаться к значению EVPI. При бинарном или равномерном распределении эта кривая обычно выгнута сильнее, чем при нормальном, поэтому с каждым новым измерением EVI растет быстрее.

Таким образом, стоимость информации, снижающей неопределенность вдвое, обычно превышает половину EVPI. В нашем примере с рекламной кампанией EVPI составляла 337 500 дол. Если вы считаете, что, потратив на исследования в 150 000 дол., удастся сократить неопределенность вдвое, то ваше исследование экономически оправданно (хотя, возможно, и не полностью). А если вы сумеете провести измерение за 30 000 дол., то это, очевидно, будет большой удачей.

Еще одна особенность кривой EVI, о которой необходимо помнить, особенно в случае равномерного распределения, заключается в следующем: график равномерного распределения плоский, резко обрывающийся на границах; значения за этими границами невозможны, а все значения внутри них равновероятны. Когда калиброванный эксперт желает отнести наш интервал (100 тыс. — 1 млн проданных единиц продукции) к равномерному распределению, этим он, в сущности, говорит, что вероятность продать больше 1 млн или меньше 100 тыс. единиц продукции равна нулю. Если мы сумеем осуществить измерение, которое, по крайней мере, позволит поднять нижнюю границу до уровня, превышающего порог в 200 тыс. проданных единиц продукции, то возможность убытков будет устранена. В такого рода примерах EVI быстро растет до точки, в которой неопределенность снижается ровно настолько, что появляется возможность устранить вероятность потерь. Разность между стоимостью информации, снижающей неопределенность вдвое и снижающей ее на три четверти, может оказаться весьма небольшой. Как только мы устраним возможность убытков (или определим наверняка, что их избежать не удастся), стоимость результатов любых дополнительных измерений окажется намного ниже.

Хотя описанный метод расчета EVPI с помощью рисунка 7.2 для нормальных распределений является аппроксимацией, погрешность ответа при нормальном распределении не должна превышать 10 %. Можно определить ожидаемую стоимость информации, помня о том, что она не должна превысить EVPI, и зная общую форму кривых EVI. На первый взгляд, мы нагромождаем одно приближение на другое, но в итоге получается достаточно точная оценка. Сам по себе расчет EVPI для предложенного измерения включает некую неопределенность, поэтому точность в расчете EVI не имеет большого смысла. Кроме того, стоимость информации о тех величинах, которые необходимо оценить, обычно очень высока. Нередко она в 10 или даже в 100 раз превышает стоимость результатов оценки менее важных переменных. Погрешность оценки EVI обычно ни на что не влияет.