Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]

Однако я убежден, что мы часто добиваемся лучших результатов, чем даже «оптимальные» линейные модели. Регрессионные модели, используемые мной для бизнеса, обычно подчиняются нескольким правилам, например такому: «Продолжительность реализации проекта является фактором дифференциации, только если она превышает год. Все проекты, реализуемые в течение года и менее, одинаково рискованны». В этом смысле такие модели не вполне линейны, но позволяют выявлять более тесную корреляцию, чем строго линейные модели линзы. Все модели, о которых Доуз упоминает в своей статье, строго линейны, но, как правило, дают более низкие значения корреляции, чем те, что я получаю с помощью нелинейных моделей.

Одним правилам меня научили эксперты, другие я сформулировал сам, проанализировав их оценки. Например, если специалист, анализирующий вероятность существенного расширения содержания разрабатываемого программного обеспечения, говорит мне, что не проводит грань между проектами, продолжительность которых составит менее года, то я просто не использую в качестве переменной исходную «продолжительность проекта». Взамен я так изменяю эту функцию, чтобы любое значение продолжительности до 12 месяцев было равно 1, 13 месяцев — 2, 14 месяцев — 3 и т. д. Но если эксперт мне этого и не скажет, то я догадаюсь обо всем по его оценкам. Предположим, что мы нанесли экспертные оценки на график зависимости вероятности значительного (требующего, скажем, увеличения объема работ более чем на 25 %) изменения спецификаций от продолжительности реализации проекта (в месяцах). Получим следующую картину (см. рис. 12.4).

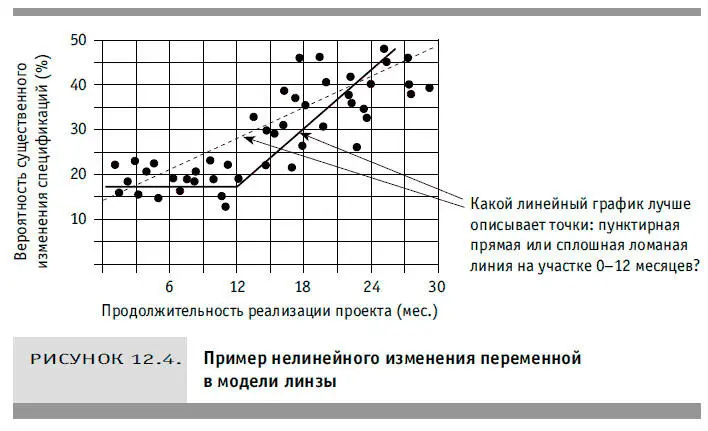
Если вам кажется, что геометрическим местом этих точек служит, скорее, пунктир, то вы не одиноки в своем мнении. Оценивая проект, на реализацию которого уйдет больше года, придется учесть другой набор факторов. Возможно, с точки зрения эксперта, одни переменные больше или меньше зависят от продолжительности проекта. Модель линзы, учитывающая эти нелинейные зависимости, не только лучше соответствует мнениям специалистов; еще важнее, что она лучше коррелирует с фактическими результатами.

Бывает также, что удачный выбор переменной требует использования еще более сложных правил. Иногда существует тесная корреляция зависимой переменной не с самой независимой функцией, а с ее логарифмом, с обратной к ней величиной или с ее отношением к произведению других независимых переменных. Эксперименты в этой области только приветствуются. Как правило, я пробую несколько вариантов линейных переменных для одних и тех же исходных данных и обычно обнаруживаю, что один из них явно выигрывает на фоне других.

Оказывается, что вы можете пользоваться моделями взвешенных оценок разной степени сложности. Если не боитесь экспериментировать с нелинейными методами, то вам подойдут именно они. Если это для вас слишком сложно, но вы разбираетесь в линейной регрессии, то применяйте ее. Если вы не знакомы с регрессионным анализом, то в вашем распоряжении z-показатели Доуза с одинаковыми весами. Каждый из этих методов эффективнее другого, более простого, и все они эффективнее, чем обычная оценка эксперта.

Самое главное — никогда не используйте метод, способный увеличить ошибку первоначальной оценки.

Кое-кто из читателей может подумать: до сих пор автор пытался снизить планку требований к измерениям настолько, что одно только это сделает измеримым любой объект или явление. Ведь я с самого начала заявил: измерением может считаться все, что снижает неопределенность. Разнообразные ошибки наблюдения — вовсе не препятствие, если только неопределенность после измерения ниже, чем до него. Даже методы анализа того, что обычно считается «субъективным» (например, модель Раша и модель линзы), — тоже измерение, если есть убедительные доказательства, что они действительно позволяют получать более точные оценки. Вместе с тем существуют такие способы, которые я не могу считать измерением даже при этих отнюдь не жестких критериях. Поэтому сейчас, прежде чем перейти к описанию новых методов количественной оценки, я хочу благоразумно притормозить и сделать ряд оговорок.

Раз не нужно больше заботиться о точности измерения, наше определение его как «снижение неопределенности», безусловно, делает выполнимой оценку чуть ли не всего, что угодно. Но это определение предполагает и строгое ограничение. Если какой-то метод на самом деле не уменьшает неопределенность или, более того, ее увеличивает, то это нельзя считать измерением и его ценность для принимающих решение равна нулю. В подобном духе запоздалого измеренческого скепсиса мы должны обсудить два весьма распространенных метода измерения: анализ «затраты/выгоды» и метод субъективных взвешенных показателей.