Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]

Сама семиэтапная процедура расчетов довольно проста. Я слегка изменил ее, чтобы учесть и другие методы (например, калибровку вероятностей), ставшие известными после того, как Брунсвик разработал свой способ (см. рис. 12.3).

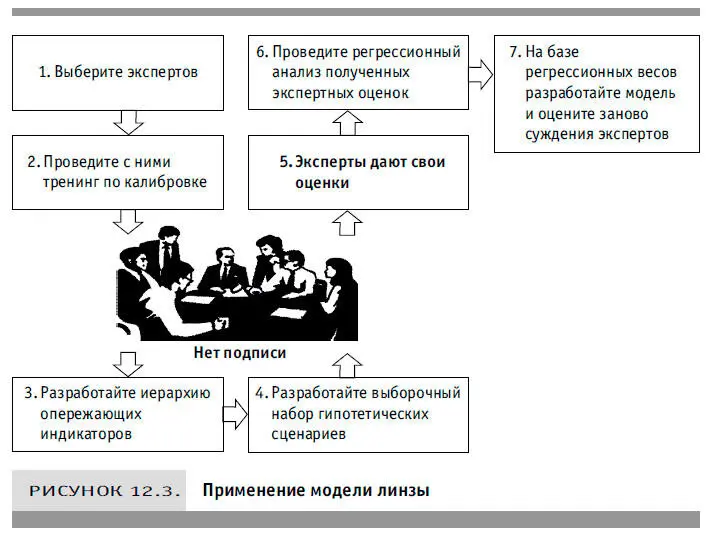
1. Выберите экспертов, которые будут участвовать в процессе.

2. Если им придется оценивать вероятность или интервал значений, то калибруйте их.

3. Попросите экспертов составить список (не более чем из 10 пунктов) факторов, требующих учета при вынесении оценки (например, «продолжительность реализации проекта разработки программного обеспечения повышает риск неудачи» или «уровень доходов лица, обращающегося за ссудой, влияет на вероятность погашения им взятого кредита»).

4. Разработайте ряд сценариев с разными сочетаниями значений каждого из выявленных факторов воздействия. За основу можно взять и реальные, и чисто гипотетические примеры. Составьте по 30–50 сценариев для каждого эксперта.

5. Попросите экспертов дать оценку каждого сценария.

6. Проведите регрессионный анализ, следуя указаниям, изложенным в главе 9. Независимые переменные «Х» — предоставленные экспертам исходные данные. Зависимая переменная «Y» — оценка, которую должен был дать эксперт.

7. Программа Excel создаст таблицу результатов, в которой вы найдете коэффициент для всех столбцов данных из ваших сценариев. Найдите коэффициент, соответствующий каждой переменной, умножьте ее на этот коэффициент, а затем суммируйте все полученные таким образом произведения. Это и есть величина, которую вы пытаетесь измерить.

Результатом процедуры, описанной выше, является таблица с весами для всех переменных, входящих в модель. Поскольку данная модель внутренне непротиворечива, мы знаем, что уменьшили ошибку, по крайней мере частично.

Быстро выяснить, насколько модель линзы снижает неопределенность, можно, оценив непоследовательность экспертных суждений. Для этого нужно предложить экспертам дублирующие друг друга сценарии, что должно остаться для них в тайне. Иными словами, седьмой и двадцать девятый сценарии в списке могут быть одинаковыми. Изучив два десятка сценариев, люди забудут, что уже знакомы с этой ситуацией, и вполне могут дать отличающийся ответ. Вдумчивые эксперты обычно последовательны в своих суждениях о сценариях. Тем не менее именно непоследовательностью объясняется 10–20 % ошибок большинства экспертных оценок, их полностью устраняет метод линзы.

Поборник простых, неоптимизированных линейных моделей Робин Доуз согласен с тем, что Брунсвик добился значительного улучшения по сравнению с обычными суждениями экспертов. Вместе с тем он утверждает, что такой результат вовсе не связан с определением «оптимальных» весов при помощи регрессии. В своей статье Доуз на четырех конкретных примерах показал, что модель линзы дает лишь небольшое улучшение по сравнению с моделями, которые он назвал «неправильными», где веса факторов не выводятся из регрессии, а считаются одинаковыми или, как это ни странно, приписываются случайным образом [45] Robyn M. Dawes, Bernard Corrigan. Linear Models in Decision Making // Psychological Bulletin, 1974, Vol. 81, № 2, p. 93–106. .

Доуз пришел к выводу, что главная ценность экспертов заключается в том, что они определяют подлежащие учету факторы и относят их к «хорошим» или «плохим» (то есть решают, будут ли их веса иметь знак «плюс» или «минус») и что рассчитывать точные значения этих весов с помощью регрессии вовсе не обязательно.

Приведенные Доузом примеры, возможно, и не позволяют судить об эффективности модели линзы как инструмента решения задач, возникающих в бизнесе [46] По крайней мере, в одном из четырех примеров «экспертами» были студенты. В двух остальных примерах эксперты предсказывали мнения других специалистов (патологи предсказывали диагнозы других врачей, а преподаватели предсказывали оценки приемной комиссии). Кроме того, большинству экспертов, на основе оценок которых была построена первая модель, удалось предсказать результаты несколько лучше, чем это было сделано с помощью баллов Доуза. , но его выводы все равно полезны. Во-первых, собственные данные Доуза доказывают определенное преимущество, пусть и небольшое, оптимальных линейных моделей над «неправильными» моделями. Во-вторых, его выводы подтверждают ту мысль, что некая непротиворечивая модель (с оптимизированными весами или без них) лучше, чем единственно человеческое суждение эксперта. И все же я думаю, что усилия по созданию оптимальных моделей, особенно когда нужно принять действительно важное решение, вполне оправдывают даже то небольшое улучшение, которое они обеспечивают по сравнению с более простыми моделями.